an elementary approach to the
default probability using Merton
model
マートン・モデルに基づいて倒産確率を計算する方法を探究してみた。この分野では正確な理解のためにはウイナー過程といった確率過程や伊藤の公式(Ito's lemma)などの数学的知識が要求されるようだ。しかし、そこまで至らなくても、大体どのような手順で倒産確率を計算しているのかを知っておくのも面白いと思い、数学の素人がエクセルを使って分かる範囲で探ってみた。
複式簿記の原理で広く知られていることだが、貸借対照表では企業の資産は負債と株主資本(純資産)の合計に等しい。
資産(V)=負債(B)+株主資本(S)
この関係は時価ベースでも成立するが、常時、このような数値を観測することは株式時価を除いては不可能である。上場企業といえども決算発表は年に4回であり、日々の企業の資産価値を知ることはできないし、ましてや秒単位の変動など観測不能である。しかし上場企業であれば株式の時価は観測できるので
株価×発行済株式数=株主資本(時価ベース)も観測可能となる。話を単純にするため負債は満期日に一括返済する額面Bの割引債とする。満期日の返済額はBと分かっているが現在の時価は未知数となる。従って、現時点では
V(未知数)=B(その時価は未知数)+S(観測可能で既知)
という関係が成り立っている。
マートンモデルでは満期日に資産から負債を返済するが満期時点で
資産(V)>負債(B)
であれば資産から負債を完済し、残りは株主価値となる。
資産(V)<負債(B)
であれば株主は株主持分を放棄して何も得ないが株主有限責任でそれ以上の損を被ることはない。しかし、債権者は回収不能部分だけ損失を受ける。このような状態を倒産と解釈することができる。算式で整理すると
このようなペイオフの関係はヨーロッパ型コールオプションの満期日のペイオフと同じであり、株式を、資産(V)=原資産、負債(B)=権利行使価格、株式時価=コールプレミアム といったコールと見なすことができる。
ヨーロッパ型コールオプションと同じペイオフとなれば有名なブラック・ショールズの公式にこれをあてはめることができる。マートンはこの公式の前提に加えて資産Vは幾何ブラウン運動に従うと仮定した。
ここからはブラックショールズモデルのコールオプション価格の算式を使って検討してみる。参考文献として
John C Hull(2003) Options, Futures, and Other Derivatives, Prentice Hall
のchapter 26 credit riskを参考にしている。最近の改定版では章が変わっているかもしれない。
資産(V)=原資産、負債(B)=権利行使価格、株式時価=コールプレミアム として
ブラックショールズ式にあてはめると以下のようになる。
この式をEQ-A としておく。
ブラックショールズ式におけるN(d2)は満期日にin the money(ITM)つまり権利行使される確率と解釈される。ここでは 資産(V)>負債(B) の状態にある確率と解釈される。従って権利行使されない確率、つまり 資産(V)<負債(B) の状態になる確率は 1-N(d2) で計算できる。これが倒産確率と解釈できる。
正規分布の密度関数は釣鐘状で左右対称なので累積分布関数では
1-N(d2)=N(-d2)
の関係が次図のように成立する。
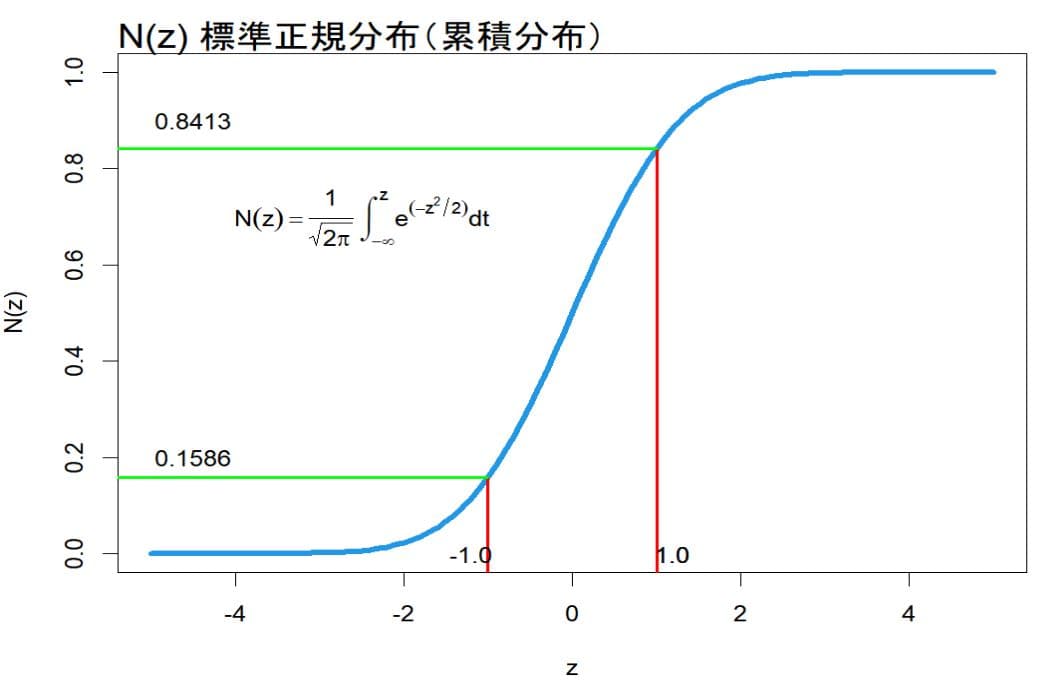
グラフから、N(-1)=0.1586 N(1)=0.8414と読める。正規密度関数を-∞から∞まで積分すると N(∞)=1
正規密度関数を-∞から-1まで積分すると
N(-1)=0.1586
正規密度関数を-∞から+1まで積分すると
N(1)=0.8414
となることを表している。
エクセルの関数NORMSDIST()を使って
NORM.S.DIST(-1,TRUE) =0.1586
で検算できる。
マートンは
V(未知数)=B(未知数)+S(観測可能で既知)という式で表されるVつまり資産は幾何ブラウン運動に従うと考えるので
dV=μVdt+σvVdW
といった確率微分方程式で表す。
ここで
V=資産(企業価値)
σv=資産価値のボラティリティ
μ=資産の期待収益率
dW は標準ウイナー過程を表す。
マートンのアイディアは観測不能な資産(企業価値)時価とそのボラティリティを未知数として、ブラックショールズ式に観測可能な株式時価を与えることで解を求めようとするものである。ちょうどインプライドボラティリティをブラックショールズ式にコール価格を与えて逆算するような考え方である。インプライドボラティリティの場合は未知数がボラティリティ 1個であったが、資産とそのボラティリティという未知数が2個なので、ブラックショールズ式の他にもう一つの方程式を導いて2本の非線形連立方程式を組み立てることで解を求めようとする。
株価(ブラックショールズ式にあてはめるときにはコールプレミアムと見なされる)は資産V(幾何ブラウン運動をすると仮定されている)から成る合成関数になるので、伊藤の公式(Ito's lemma)を適用することができる。
株価もウイナー過程に従うので
dS=μsSdt+σSSdW
S=株価
σv=株式ボラティリティ
μs=株式の期待収益率
dW は標準ウイナー過程
で表す確率微分方程式で表現される。
この確率微分方程式に伊藤の公式を適用してVで合成関数を微分するような感覚(数学的には著しく不正確な表現かもしれないが)で確率微分方程式を変形すると以下のように表せる。金融工学の世界では定石のごとくよく使われる数式操作に感じる。
dS=μsSdt+σSSdW とその変換された確率微分方程式は同じなのでdWの項は等しいはずである。
そこから
の関係式が導かれる。
ブラックショールズ式ではデルタが
で表せるので下記のような、もう一本の方程式が導出できる。
この式をEQ-B としておく。
EQ-AとEQ-Bの2本の方程式から資産VとそのボラティリティσV を求める作業となる。非線形の連立方程式で代数的には解けないので数値計算で解を近似計算する。ここではエクセルのソルバーを使うことにする。
Hullのテキストの設例をsolverで解いてみる。
計算例はHullのテキストの設例を利用することにする。S(株価)=3
V(資産)=未知数
B(満期日の負債)=権利行使価格=10
r(リスクフリー利子率)=0.05
T(満期までの年数)= 1
σV 資産のボラティリティ=未知数
σS 株式のボラティリティ=0.8
ワークシートにブラックショールズ式の計算式EQ-Aともう一つの方程式EQ-Bを作り、それぞれが株式時価と等しくなるようにする。具体的には計2本の方程式の解と株価(既定値)との誤差の二乗和が最小となるようにソルバー使って求めることになる。式で示せば
ワークシートの作り方は各自の好み次第であるが、ちなみに一例を示しておく。マーカー部分は既知数である。ソルバーを起動する前に未知数であるVとstd(V)つまりセル$C$3と$C$9には仮の暫定値として1をそれぞれ入力しておく。
ワークシート(計算結果)
ソルバーの設定例
ワークシートの数式表示
ソルバーの解答レポートは以下のようになる。

このようにして連立方程式を
解くことで
倒産確率=0.1269
資産価値V=12.395
が求まる。
その他にも
負債時価=12.395-3=9.395
負債Bの現在価値=10*EXP(-0.05*1)=9.512
予想損失(EL)=0.1169=
9.512-9.395
が計算できる。
予想損失をEL(Expected Loss)、倒産(デフォルト)確率をPD、倒産時点での貸付金時価をEAD(Exposure at default)、倒産した場合の損失率LGD(Loss given default)とすると、予想損失ELは以下の式で示せる
EL=PD x LGD x EAD =PD x (1-RR) x EAD
従って
LGD=EL/EAD/PD=
0.1169/9.512/0.1269=
0.0967
RR=1-LGD=1-0.0967=0.9032
なども計算できる。
ここで債権者の立場、つまり割引債Bに10を投資している立場からみると、割引債の時価は一物一価の法則が成立する世界では上記の計算のように理論的に9.395となる。満期には10の返済が見込まれるが、その現在価値は9.512なので時価ベースで考えた予想損失(EL)は9.512-9.395=0.1169となる。ここで債権者は0.1169について貸倒引当金を計上すべきとする考えも出てくるだろう。この辺は会計理論とファイナンス理論の融合をどのように考えるかという大きなテーマになってくるのだろう。
マートンの当初のモデルでは満期日の倒産確率しか計算できないが、負債を満期に一括返済するのでなく段階的に返済する場合や満期日前の倒産確率が計算できるような拡張モデルも開発されており、大手格付け会社により商標登録されているモデルもあるようだ。しかし基本的な考え方はマートンのオリジナルのモデルがベースとなっているようだ。
参考付録(LibreOffice Calcのソルバーで解いてみる)
LibreOffice Calcでソルバーを使う場合はJavaの実行環境が必要となる。java(JDK)のインストールについては例えばjavaの公式サイト https://www.java.com/ja/ や放送大学のhttps://info.ouj.ac.jp/~maps17/software/などを参考にして自己責任で試みられたい。LibreOffice
Calcのソルバーを使う場合は「変化させるセル」が飛び地になっているとうまく機能しないようなので「変化させるセル」を隣接するようにワークシートのデザインを若干修正している。 またターゲットセルをゼロにするように設定し、冗長な制約条件を付けずに解を求めてみた.変化させるセル$C$3,$c$4には暫定値として1を入れておく。ソルバーで解くと以下のようになる。
LibreOffice Calcの計算結果
ワークシートの数式表示
LibreOffice Calcのソルバーの設定
エクセルのソルバーと似たような解が得られた。
参考文献
John C Hull(2003) Options, Futures, and Other Derivatives, Prentice Hall
蓑谷千凰彦(2000)よくわかるブラック・ショールズ・モデル 東洋経済新報社
小山昭雄(1999)経済数学教室 別巻 確率論 岩波書店
Merton, R. C. (1974). On the pricing of corporate debt: The risk structure of interest rates. The Journal of finance
ブラック・ショールズ・モデルのデルタ導出とN(d1)、N(d2)の考え方 deriving Black Scholes option's Delta
標準正規分布グラフと標準化normal distribution plot in MAXIMA