幾何ブラウン運動 Rによる初歩的計算例
simple simulation of geometric brownian motion using
R.
幾何ブラウン運動のシミュレーションを行ってみた。Rには専門的なパッケージが揃っているので、わざわざ稚拙なプログラムを作る必要はないかもしれないが、頭の筋トレのつもりで試作してみた。
自作プログラムの検証にはパッケージを使い出力結果を比べてみて多分、大丈夫だろうと判断した。シミュレーションはブラックショールズ過程による幾何ブラウン運動で行っている。
ブラックショールズモデルの下記の確率微分方程式に従っている。
μは移動係数(瞬間的な期待収益率)、σは瞬間的なボラティリティで標準偏差、dzはウイナー過程としてdSは株価の微小な変動を表す。
ztはウイナー過程
S0は初期株価
STはT時点での株価
とすると、上記の確率微分方程式の解は
ここでシミュレーション回数10回(つまり軌跡を描く本数)、μ 0.15 σ 0.3 として計算しグラフを描いてみる。
nsim <- 10 # シミュレーション回数(必要な軌跡グラフの本数)
m<-0.15
# パラメータ- 利子率 瞬間的期待収益率 drift係数などと呼ばれている。
sigma<-0.3 # パラメーター ボラティリティ
x0<-35 # 初期価格
n<-250 # 時間刻み数 仮に1年を250営業日数と仮定すれば 1/250 がδt
T<-1 # 最終時間 仮に1年間としていつ。
time<-seq(0,T,by=T/n)
set.seed(1)
B <- matrix(rnorm(nsim * n, 0, 1/sqrt(n)), nsim,
n,byrow=T)
BM <- apply(B, 1, cumsum)
BM1<-rbind(numeric(nsim),BM)
tcc<-(m-0.5*sigma^2)*time
BM2<-tcc+BM1*sigma
expss<-x0*exp(BM2)
matplot(expss,type="l",lwd=2)
lines(0:n,rowMeans(expss),col="red",lwd=4)
確率微分方程式に関連するシミュレーションを行うパッケージSim.DiffProcを使って上記と同様のシミュレーションを行ってみた。
###パッケージ Sim.DiffProc を使ったシミュレーション
suppressMessages(library(Sim.DiffProc))
## Brownian motion
set.seed(1)
X <- GBM(N =250,M=10,theta=0.15,sigma=0.3,x0=35)
plot(X,plot.type="single")
lines(as.vector(time(X)),rowMeans(X),col="red",lwd=4)
シミュレーションの計算結果の一部を比較すると
head(expss)
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9]
[,10]
[1,] 35.000 35.000 35.000 35.000 35.000 35.000
35.000 35.000 35.000 35.000
[2,] 34.601 35.105 35.066 34.061 35.777 35.058
35.584 35.183 34.431 35.828
[3,] 34.736 35.392 34.884 33.533 36.555 35.769
34.979 35.206 33.212 35.334
[4,] 34.204 35.361 34.124 32.761 35.971 37.352
35.592 33.925 34.263 34.917
[5,] 35.270 35.210 34.145 33.192 36.130 38.311
34.977 33.665 34.616 34.763
[6,] 35.506 35.692 34.808 32.403 36.193 37.700
35.352 34.073 34.594 33.933
head(X)
X1 X2 X3 X4 X5 X6 X7 X8 X9 X10
[1,] 35.000 35.000 35.000 35.000 35.000 35.000
35.000 35.000 35.000 35.000
[2,] 34.601 35.105 35.066 34.061 35.777 35.058
35.584 35.183 34.431 35.828
[3,] 34.736 35.392 34.884 33.533 36.555 35.769
34.979 35.206 33.212 35.334
[4,] 34.204 35.361 34.124 32.761 35.971 37.352
35.592 33.925 34.263 34.917
[5,] 35.270 35.210 34.145 33.192 36.130 38.311
34.977 33.665 34.616 34.763
[6,] 35.506 35.692 34.808 32.403 36.193 37.700
35.352 34.073 34.594 33.933
と同一の結果を得た。
赤色の太線は各時点での株価の期待値を表している。おおむね初期価格の近傍にある。これは幾何ブラウン運動のマルティンゲール性を表現しているとも解釈できるだろう。
ドリフトなしの幾何ブラウン運動
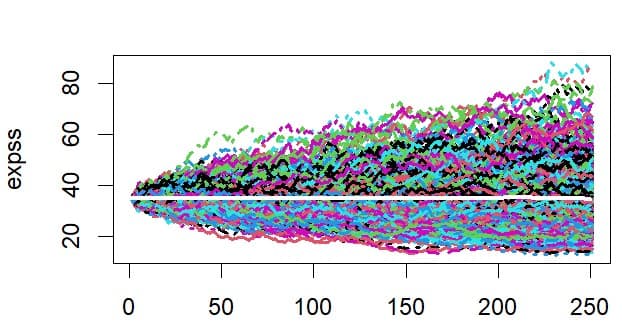
次にシミュレーション回数を1000回にして、ドリフトがない場合、μ=0 σ= 0.3 初期価格=35で計算しグラフを描いてみる。
nsim <- 1000 # シミュレーション回数(必要な軌跡グラフの本数)
m<-0.0 # パラメータ- 利子率
sigma<-0.3 # パラメーター ボラティリティ
x0<-35 # 初期価格
n<-250 # 時間刻み数
T<-1 # 最終時間
time<-seq(0,T,by=T/n)
set.seed(1)
B <- matrix(rnorm(nsim * n, 0, 1/sqrt(n)), nsim,
n,byrow=T)
BM <- apply(B, 1, cumsum)
BM1<-rbind(numeric(nsim),BM)
tcc<-(m-0.5*sigma^2)*time
BM2<-tcc+BM1*sigma
expss<-x0*exp(BM2)
matplot(expss,type="l",lwd=2)
lines(0:n,rowMeans(expss),col="white",lwd=3)
下記のグラフを得る。
hist(expss[15,],freq=F,breaks =
seq(min(expss[15,]),
max(expss[15,]), length.out = 31))
lines(density(expss[15,]),lwd=5,col="cyan")
hist(expss[151,],freq=F,breaks =
seq(min(expss[151,]),
max(expss[151,]), length.out = 31))
lines(density(expss[151,]),lwd=5,col="cyan")
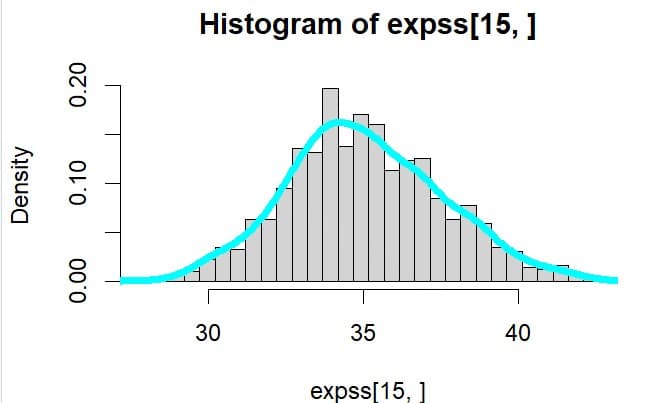
時点15でのヒストグラムは
平均値と標準偏差は
> mean(expss[15,])
[1] 35.05578
> sd(expss[15,])
[1] 2.493466
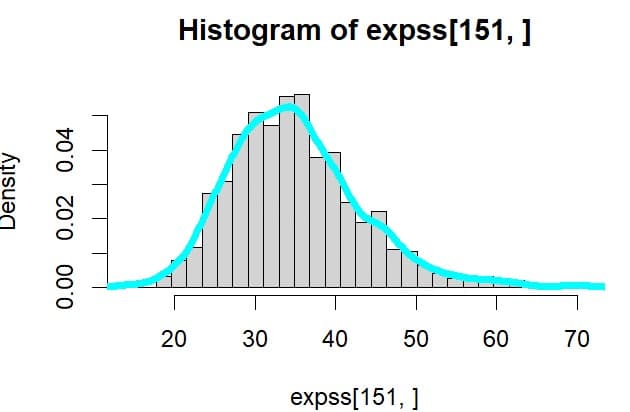
時点151でのヒストグラムは
平均値と標準偏差は
> mean(expss[151,])
[1] 35.00053
> sd(expss[151,])
[1] 8.174799
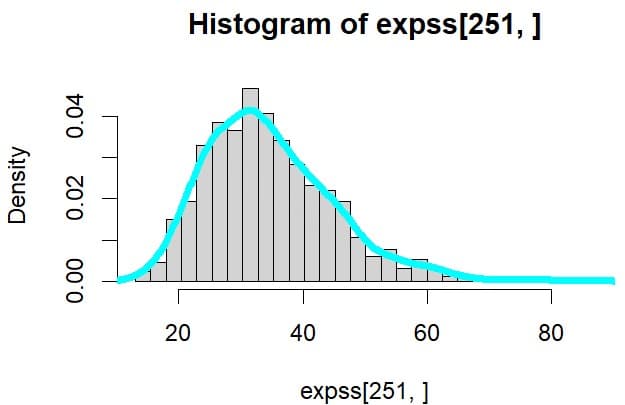
時点251でのヒストグラムは
平均値と標準偏差は
> mean(expss[251,])
[1] 34.76948
> sd(expss[251,])
[1] 10.55669
上記のようなブラックショールズ過程に従う株価の時点ごとの期待値と分散は次のように表される。(数式の導出は参考文献2蓑谷を参照)
期待値
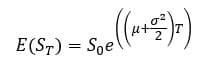
分散
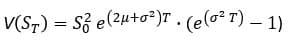
時点151について上式に当てはめてみる。
初期価格=35
μ=0 σ=0.3
時間刻みは1/250=0.004
従って微少の単位時間あたりのσ=0.01897=0.3/√250
時点151の経過時間はt=0.604=151*0.004
以上からT-151における株価の期待値は
35.0038=35*EXP((0+0.5*0.01897^2)*0.604)
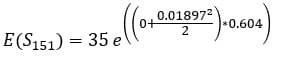
分散についても上記の数式に当てはめると
0.26635=35^2*EXP((2*0+0.01897^2)*0.604)*(EXP(0.01897^2*0.604)-1)
![]()
分散0.26635 は微少単位時間あたりの分散なので年率に戻すには250*0.26635=66.587となる。標準偏差はその平方根なので√66.587=8.16008 となる。シミュレーションで得た時点151の平均値は35.0053、標準偏差は8.174なのでよく近似している。
いずれの時点での株価のヒストグラムは対数正規分布の形に近く見える。平均値も35近辺にあり、標準偏差は時間が進むとともに大きくなっているとがわかる。株価については、いつの時点でも期待値は初期価格に等しいというマルチンゲール性が示されている。
ドリフト付きの幾何ブラウン運動
シミュレーション回数を1000回にして、ドリフトがある場合、μ=0.25 σ= 0.3 初期価格=35で計算してグラフを描いてみる
上記のRコードを m<-0 から m<-0.25に書き換えるだけで下記のグラフを得た。
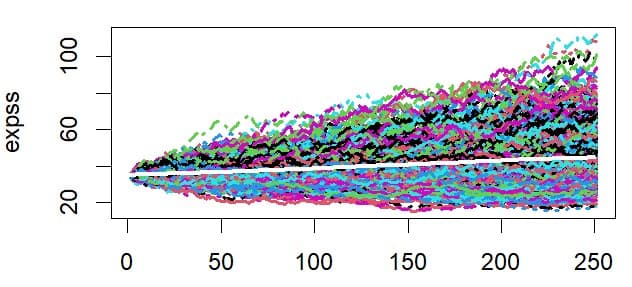
白色の太線は各時点での株価の期待値を表している。ドリフトのμ=0.25
を反映して、やや右肩上がりの直線に描かれている.
このような拡散過程も測度変換を使うとマルティンゲールとなるようだ。
時点15での株価のヒストグラムは
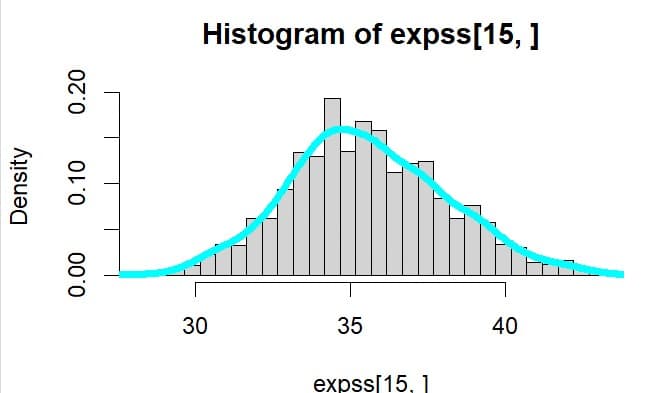
平均値と標準偏差は
> mean(expss[15,])
[1] 35.55001
> sd(expss[15,])
[1] 2.52862
時点151での株価のヒストグラムは
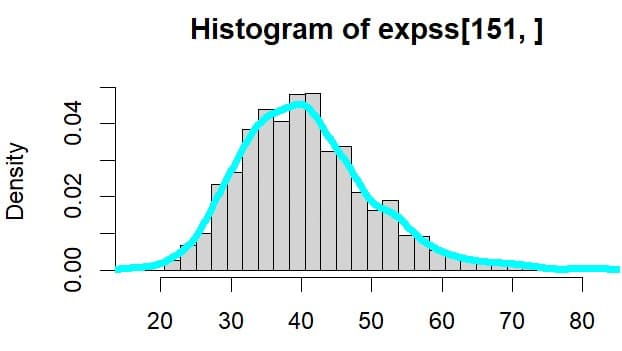
平均値と標準偏差は
> mean(expss[151,])
[1] 40.66481
> sd(expss[151,])
[1] 9.497762
時点251での株価のヒストグラムは
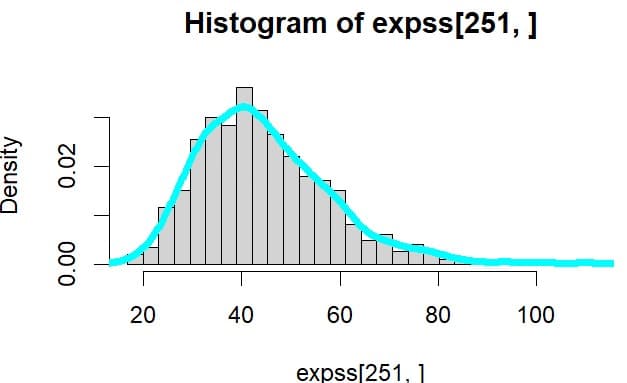
平均値と標準偏差は
> mean(expss[251,])
[1] 44.64489
> sd(expss[251,])
[1] 13.55506
上記のブラックショールズ過程に従う株価の時点151についての期待値と分散は下のようになる。
時点151について期待値と分散の下記の式に当てはめてみる。
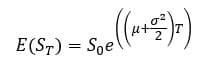
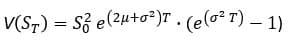
初期価格=35
μ=0.25 σ=0.3
時間刻みは1/250=0.004
従って微少の単位時間あたりのσ=0.01897=0.3/√250
時点151の経過時間はt=0.604=151*0.004
以上からT-151における株価の期待値は
40.709=35*EXP((0.25+0.5*0.01897^2)*0.604)
分散についても上記の数式に当てはめると
0.36025=35^2*EXP((2*0.25+0.01897^2)*0.604)*(EXP(0.01897^2*0.604)-1)
分散0.36025 は微少単位時間あたりの分散なので年率に戻すには250*0.36025=90.063となる。標準偏差はその平方根なので√90.063=9.49 となる。シミュレーションで得た時点151の平均値は40.66、標準偏差は9.498なのでよく近似している。
シミュレーションから得た各時点の平均値を対数変換してグラフにしてみる。
expssmean<-apply(expss,1,mean)
logprice<-log(expssmean)
plot(logprice,typ="l",lwd=3)
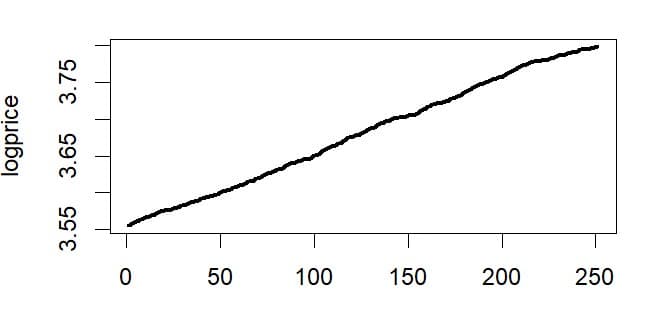
対数変換した平均値を時間で説明する回帰分析をすると
lm(logprice ~ time)
Call:
lm(formula = logprice ~ time)
Coefficients:
(Intercept) time
3.5531 0.2541
を得る。μ=0.25に設定してシミュレーションを行っているので回帰係数0.2541はよく近似していることがわかる。
上記のようなドリフト付きの幾何ブラウン運動に従う株価は利子率rの債券価格ertで除することでドリフトがゼロの標準ブラウン運動に変換できマルチンゲールとなることが知られている。(マルチンゲールや測度変換は難しい話なので金融数理の専門的テキストを参照されたい)
ファイナンス理論ではマルチンゲール(martingale)に基づく価格モデルが使われているので、リスク資産に投資して収益を上げたいと考える人にとってあまり面白い話ではないし、リスク資産を売って手数料を稼ぎたい人にとってもセールトークには全く役に立たない話しになるので面白くない話になる。明日の株価の最良の予測値は今日の株価だと言われても有り難がる人は少ないだろう。しかし冷静に考えれば現時点までにある情報は現在価格に反映されるが、未来の価格はその時になってみなければわからないが、その条件付期待値は現時点での時価に等しいと述べているので良心的な学問ともいえる。何か特別な秘密の数式で未来の価格がわかるということになると魔術師や予言者の領域になりサイエンスの領域から逸脱してしまうだろう。リスク資産に投資する前に様々な可能性を分析する手法としてモンテカルロ法によるシミュレーションがよく使われる。上記の幾何ブラウン運動に基づくシミュレーションもその一つになるが、どのようなモデルに基づいてシミュレーションを行うかに注意をしなければならない。あまりにも恣意的なモデルを作ってモンテカルロ法によるシミュレーションを行って得た結果は信頼性に乏しくなる。上記のシミュレーションではパラメータが定数としているが、これらのパラメータが時間とともに変化するモデルによるシミュレーションも考えられる。その場合に注意すべきはファイナンス理論から見て妥当なモデルかどうかを常にチェックする必要があるだろう。
参考文献
1.John C Hull(2003) Options, Futures, and Other Derivatives, Prentice Hall
2.蓑谷千凰彦(2000)よくわかるブラック・ショールズ・モデル 東洋経済新報社
3.小山昭雄(1999)経済数学教室 別巻 確率論 岩波書店
日次の株価変動分析 状態空間モデル ローカル・リニア・トレンド・モデルを使って株価予測