日次株価変動分析 状態空間モデル・ローカル・リニア・トレンド・モデルを使って株価予測 with KFAS
analysis of daily stock price movement
using local linear trend model with KFAS
ささやかな願いと無駄話を少し
学生や一般人が日次の10年分くらいの長期株価データを入手しようとすると日本では困難に直面する。専門の組織に所属していれば商用のデータベースからデータをダウンロードできるだろうが一般的な個人には大変に難しい。海外の大学の授業案内などをネットで見ているとホームワークの課題でquantmodを使って株価データを入手してスペクトル分析を行った結果をグラフにまとめて提出せよなどと掲示されているのを見かける。日本でも米国株については同様の作業はできるが、日本企業の株価については難しい。知的財産権などをめぐる難しい問題があるのかも知れないが関係機関で共同で運営するサイトがあり、無料ないしは無料に近い料金で10年分以上の日次の始値、高値、安値、終値、出来高などのデータがダウンロード出来れば大変に便利だろうと思う。詳しい理由は知らないが、新聞には株式相場表のページがあるが使うことはない。相場表単体では使い道はなく長期の時系列データで、しかもCSVなどの電子データでダウンロード可能な形で提供されて利用価値が出て来る。
RとかOctaveなどフリーで使える統計分析ソフトは大変に充実し普及してきているが、時系列データの入手は日本では大変に難しい。金融立国を目指すならば子供でも自由にデータを入手して様々な統計分析を試みられる環境が必要だろう。米国のように自由に金融データがダウンロードできる国の市場には世界中から投資資金が流れ込んできている。ある医師の話では小さい子供にmathematicaを自由に使わせたところ、面白がって自ら数学をどんどん勉強するようになったそうだ。金融データ分析も同様で実際の生のデータを使った分析を子供や学生などに教えれば自ら学習し、数学、日本語、英語、国際問題、プログラミングなど幅広く勉強するようになるだろう。データ分析は自由な発想で仮説を立てて検証したり、推理を繰り返すのでゲームに通ずるような面白さがある。米国の学生が金融データを自由に使っているのと同様の環境を日本でも整備できれば子供達や学生だけでなく社会全体にデータ分析が広まり1億人がデータサイエンティストの素養を持つようになるかも知れない。
日次データの取扱の悩ましさ
日次データでも気象観測のように毎日一定時刻の気温を測定するのであれば計測器の不具合が無い限り欠測値は生じないだろう。しかし日次の株価は自然の物理的時間に従わないので以下のような悩ましい問題に直面する。
株価について言えば取引所の休日には取引がないので欠測値となる。いずれは24時間365日何時でも取引可能となるかもしれないが、まだその時代になっていない。日本の場合は年末年始と5月のゴールデンウイークは休日が多いのでグラフのx軸の1目盛の違いが、物理的な時間では5日間飛んでいるかも知れない。通常の株価推移グラフでは不連続に見えることがよくある。例えば12月30日の終値が1000で翌年の新年の初取引日の6日には始値が1500で窓を開けてスタートするようなことは時々見られる。前年末から1週間の間に世界各国で大きな出来事があり、それが始値に一括して反映される。逆に過去6日間に大事件があって海外では株価が大きく乱高下したものの結局年末レベルの株価に一時的に落ち着いたということもあるだろう。その場合は日本の市場での始値も前年末の終値近辺になるかもしれない。海外市場の株価グラフを見ればこの間の事情や推移が表現されているが、日本の市場のグラフだけで見れば平穏な相場に見えてしまい判断を誤るかも知れない。
月次や四半期のデータは年間のサイクルが固定しているので時系列分析では扱いやすいが日時データ特に市場の価格データは処理が難しいうえに、統計ソフトの関数によっては日付属性の付いているデータだとエラーになったり警告が出ることがよくある。この様な場合には事前にプレーンな数値ベクトルに変換する作業が必要で面倒である。日次データでは気を使うことが多くなり何かと作業に時間がかかってしまい大変悩ましいが、いづれの日にかAIが補助してくれる時期も来るのだろう。
分析用のデータについて
以下に示す分析に使ったデータはパッケージTTRにデータセットとして用意されているttrcを使った。人為的に生成された摸擬データであるが5000日分以上の始値、高値、安値、終値、出来高から成っており時系列分析には十分な量である。しかしデータが多すぎるとグラフが読みとりにくくなるので適当な期間の150サンプルを使ってみた。感覚的には円で考えると安く見えるので株価については100倍にしてある。パッケージxtsのplot.xtsは株価のような日次データをグラフ化するのには実用的で便利と感じた。
あえて利益率でなく価格水準を分析
ファイナンス理論では株価は対数正規分布に従うと仮定すること、投資家は投資規模や資産種類の影響を受けない利益率に関心を持つこと、時系列データとして定常性を満たし統計的に扱いやすいこと、などの理由で価格水準よりも ln(今日株価/前日株価)として対数変換した利益率が分析に使われることが多い。しかし、ここではファイナンス理論は一旦棚上にして価格水準そのものを分析対象にしている。ナイル川の流量を測定しその時系列変化を分析するのと同じ感覚でマーケットで計測された終値(流量に相当する)の変化に状態空間モデルを適用している。価格そのものを分析対象にすると伝統的なチャート分析(テクニカル分析)とも比較しやすいというメリットもある。
状態空間モデルとローカル・リニア・トレンド・モデルについて
状態空間モデルは統計的手法の一種で観測対象を直接に観測できない状態変数のシステムと観測値を測定する観測モデルに分離してモデリングしてパラメータを推定する手法となっている。状態空間モデルのうち、基本的でシンプルなモデルにローカルレベルモデル(local level model)がある。レベル(level)とは、たとえて言うならば単純回帰モデルY=ax+b の切片bに相当する。回帰分析の場合は分析対象期間を通して切片bは一定、つまりglobalに定数であるが、ローカルレベルモデルではこの切片が時間とともに変化する。ローカル・リニア・トレンドモデルはレベルに傾き(slope)が加わったモデルで、傾きは時間とともに変化する。
観測方程式
![]()
状態方程式 1
レベル(level)
![]()
状態方程式 2
傾き(slope)
![]()
傾きは時間とともに変化し、傾きの累積和はトレンドになり、状態方程式1に加算されていく。従ってレベルはトレンドを含む変化をする。
観測方程式、状態方程式1と2の撹乱項の分散はそれぞれ一定と仮定されている。
このモデルに株価をあてはめれるとすれば以下のように仮定する。市場価格は時に過小評価され、時に過大評価され、何かとノイズの影響を受ける。真の株価はノイズの影響を受けてるので人間には見えない。このことは観測方程式で表現されている。イメージとしては表現すれば、見えざる株価(レベル)に見えざる傾きが加わり撹乱項が加わったものが観測値Yという株価になって人間に見える。この見えざる真の株価(レベル)はノイズの影響を受けてランダムウォーク過程に従うと仮定されている。それは状態方程式1で表現されている。この状態方程式には傾き(slope)が加算されている。その傾きは同じくノイズの影響を受けてランダムウォーク過程に従うと仮定されている。それは状態方程式2で表現されている。(統計学的に正確な説明は参考文献1のブロックウエル、デーヴィスの訳書の262ページ参照。当該訳書では局所線形トレンドモデルと訳されている。)
このような状態空間モデルを最尤法を使って3つの方程式の撹乱項(誤差項)の分散や見えざる株価(レベル)傾きも推定しようとしている。もちろん、この様な仮説が御門違いの時には無意味な推定をすることになる。しかし試行錯誤によって相対的により良い仮説を追究することは意義があるだろう。(最尤法や仮説検定に関する統計哲学などについては参考文献3.
三中信宏 で詳しく論じられている。)
RのパッケージKFASを使ってttrc社の仮想の株価について状態空間モデルの推定をすると以下のようになる。
先ず150日分の株価の推移と50日移動平均線を描いてみる。
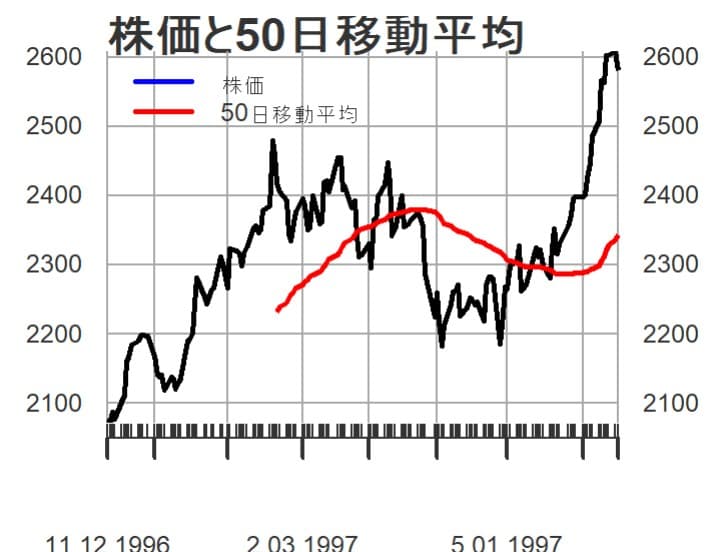
よく見かけるグラフで移動平均線はやや遅行する形になっている。
観測方程式の撹乱項の分散は12.676と推定されている。思ったよりも小さいような印象を受ける。
状態方程式1の撹乱項の分散は863と推定されている。標準偏差で見れば約29なので2000の株価がその程度に毎日変動することは不思議ではない。実際の株価指数のボラティリティが年率18%くらいのことはよく見られる。年間の取引日数を切りのよい256(16の2乗)と仮定すれば0.18*0.18/256が一日あたりの分散となり、その平方根である標準偏差は0.011になるので1日に1.1%くらい変動するのは珍しいことではない。
状態方程式2の撹乱項の分散は0.0047と推定されており実質的には一定に近い。
カルマン平滑化した株価(
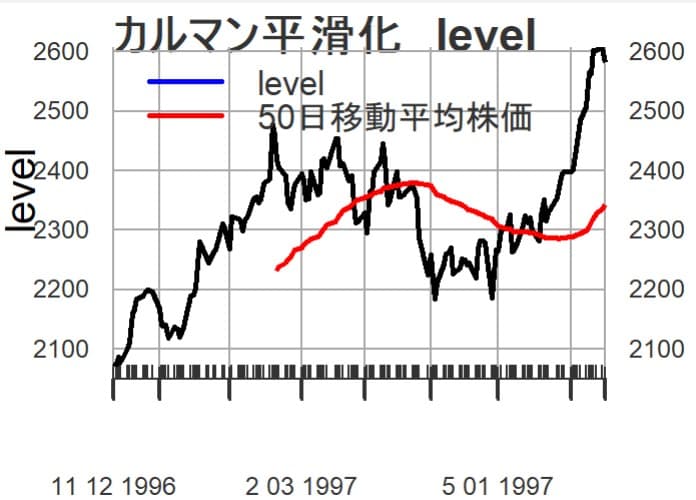
カルマン平滑化した傾き(slope)のグラフを描いてみる。
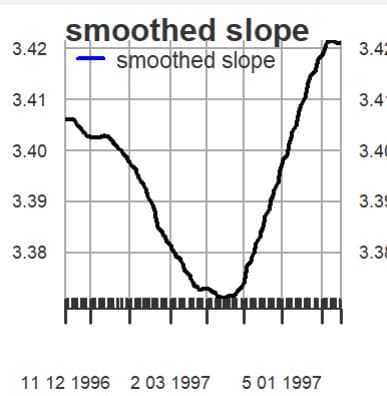
微少な数値の変化にもかかわらずグラフでは拡大鏡を通して見るようにスロープが大きく変化しているように見えてしまう。しかし株価が2000台なのでスロープの変化は非常に微少の範囲である。1997年の春頃がスロープは底を打って、その後は上向いている。この微少な傾きの変化をどの様に読むかはファンダメンタル分析やマクロ経済分析など追加的検討が必要になるだろう。
このスロープの累積和はトレンドを表すので、次にトレンドを描いてみる。
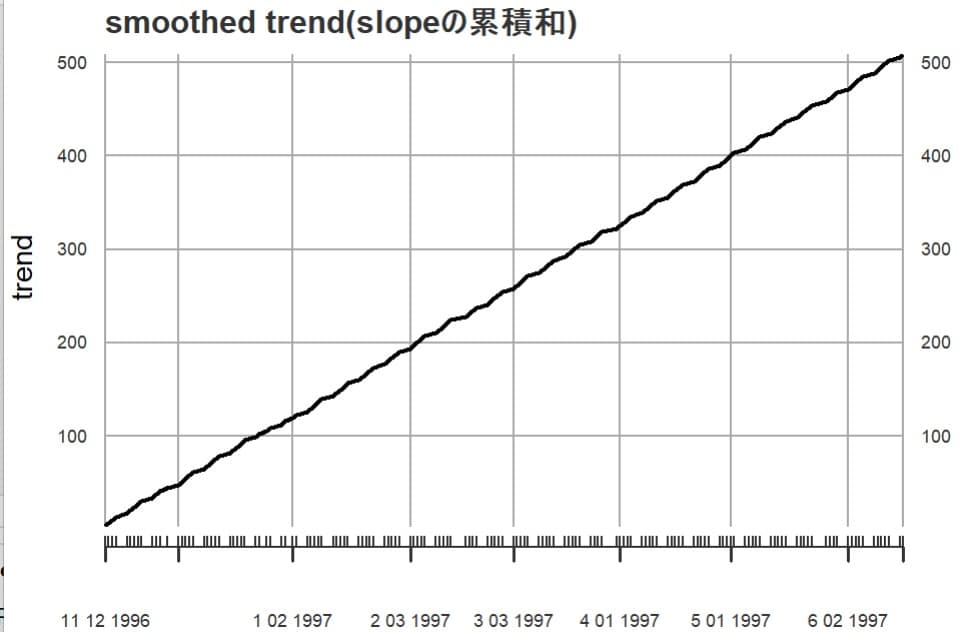
ほぼ安定して積みあがっている。
レベルからトレンドを除外したレベル(仮にpure levelと呼ぶ)と実際の株価とを比較してグラフにしてみる
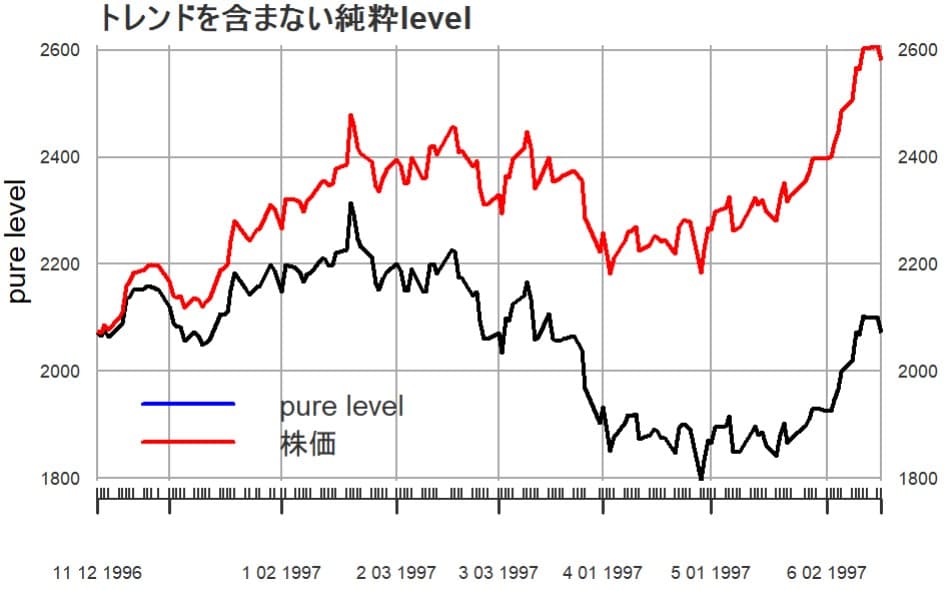
1997年の春頃からトレンドの影響が大きく現れているように見える。市場全体のトレンドの変化、その感応度の変化、銘柄選好の流れの変化などの因果関係を探るためにファンダメンタル分析が必要となるだろう。
ここまではカルマン平滑化(Kalman smoothed
estimate)推定値のため全体的に円滑なグラフであった。
ここからはカルマンフィルター化推定値(Kalman filtered
estimate)にようグラフを描いてみる。フィルタリングは現時点で利用可能な情報に基づいて現時点の状態変数を推定する。(1期前に得た当期の予測値を最新のデータで更新する。新しい観測値を入手する毎に状態変数を推定し直すアルゴリズムになっている。(カルマンフィルターの初歩的な計算例 参照)
状態空間モデルを使うと大体、過去の実績値とモデルによる予測値は近似して、グラフではほぼ重なって見えて識別しにくい。
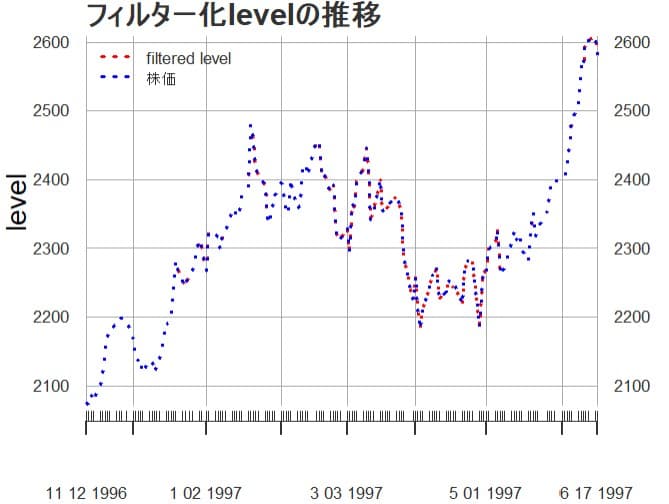
傾きのフィルター化推定値をグラフにしてみる。
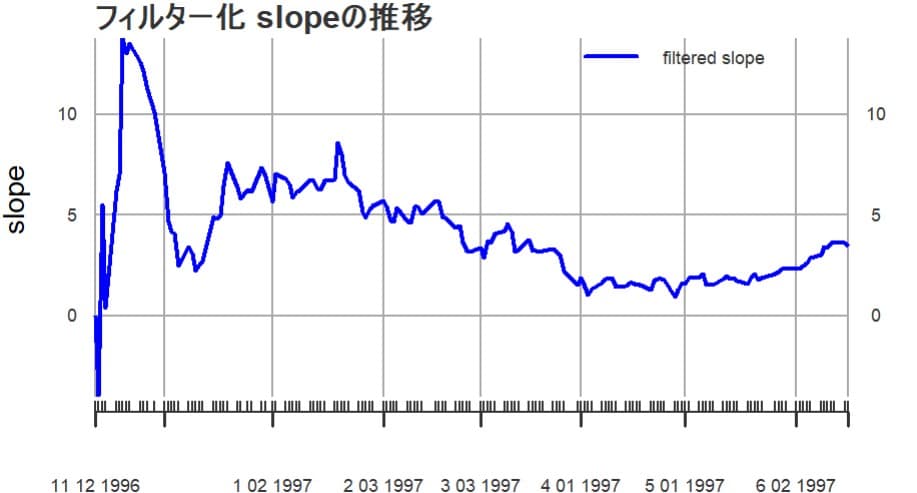
データを収集しはじめた初期頃は不安定な動きをしているが、しばらく時間がたつとなだらかな傾向が見え、1997年春頃が底で、その後は上昇傾向に見える。平滑化された推定値よりは新しいデータに対する感度がよくも見える。
トレンドは一貫して上昇傾向にある。
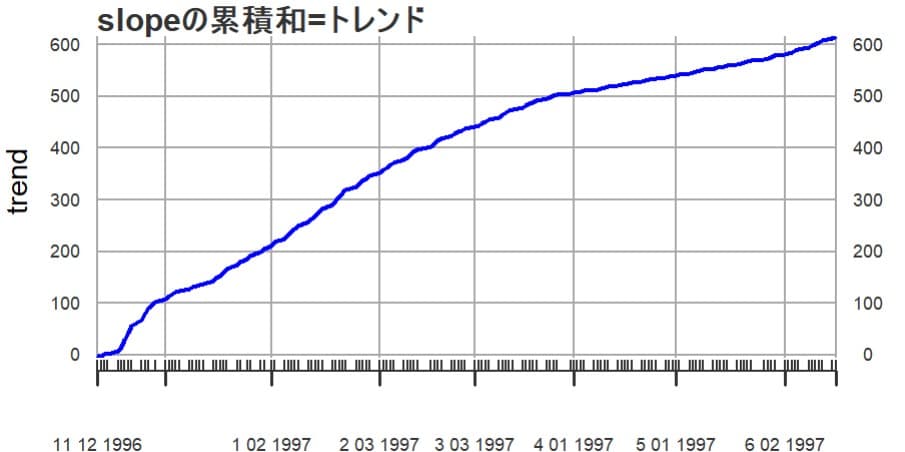
実際の株価とトレンドを除去したレベルを比較すると以下のようになる
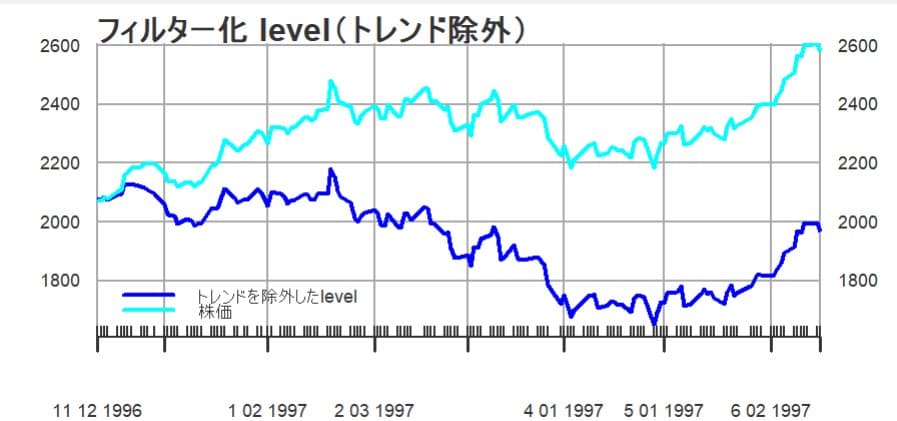
1997年の春頃に底を打って、その後は上向いている。トレンドの変化の理由などはファンダメンタル分析やマクロ経済分析などで探ることになるだろう。
株価予測について
カルマンフィルターのアルゴリズムで常に1期先の予測値が計算される。predict関数を使うと任意の期間の予測値が計算できる。1996-11-12から1997-06-17の150日間 の実際値があるので、6/18日以降の10日分のフィルター化推定値の予測値を計算してみると下図のようになる
0151-01-01 2584.855
0152-01-01 2588.276
0153-01-01 2591.697
0154-01-01 2595.118
0155-01-01 2598.539
0156-01-01 2601.960
0157-01-01 2605.381
0158-01-01 2608.802
0159-01-01 2612.223
0160-01-01 2615.644
日付表示はうまく処理できないが151日目から160日目のフィルター化推定値の予測値となっている。
グラフで表すと次のようになる。
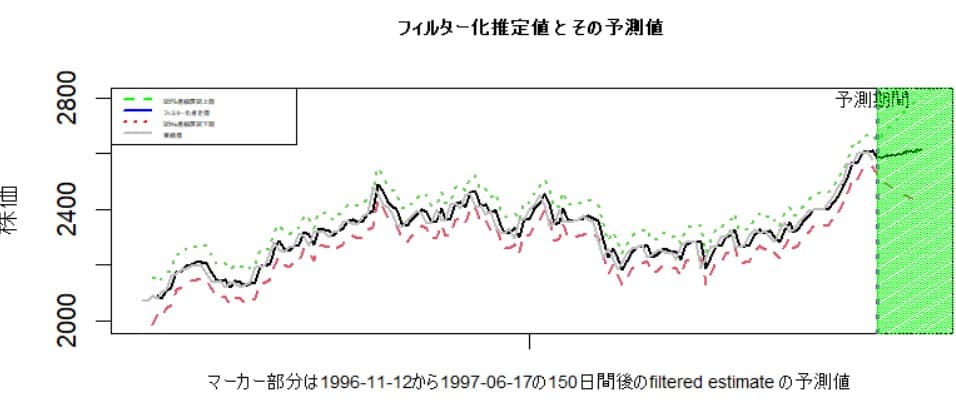
上昇傾向の予測値が計算されている。データをモデルのtraining用と予測力の検証用に分割してモデルの予測力を検証したり、cross-validationを実施することは自然科学の分野ではよく行われているようだ。しかし、欲と恐怖心に左右される株価の予測については少し注意が必要だろう。台風予測では北東に進むと予測されて台風が裏をかいてやろうと北西に進む心配は全く無い。しかし多数の人間の思惑に左右される株式市場では似たような手法の予測が出れば複雑な反応を惹起して更に予測を難しくする可能性がある。金融工学で著名な学者John
C.
Hullは有名なテキスト(参考文献4)の最終章でデリバティブ関連の過去の金融事件から学ぶべき教訓をまとめている。例えば、人は市場に勝てる(市場の先行きを正確に読める)などと思わず、事前に定めたリスク許容度(ポジションの大きさ)を真面目に守るべきと述べている。リスクを取る場合には肝に銘ずべきポイントだろう。LTCMのような過去の事案を見ると簡単な教訓を守れるかどうかは全く知能指数等とは関係がないように感じる。
状態空間モデルを使うときには機械的な予測よりも、ファンダメンタル分析やマクロ経済分析などの追加的な分析のポイントを探るために利用する方がよいかもしれない。ここでは株価についてローカルレベルモデルを
試みに適用してみたが、経済指標などで後日によく修正される傾向のある指標にローカルレベルモデルを適用して見えざる真の指標値を探るのも面白いかもしれない。このようなことをしていると昔の錬金術師の仕事の功の部分、光の部分にもっと温かい目を注ぐ必要があるとつくづく感じた。
拙文を書くために使ったRコードは以下の通り。
library(KFAS)
library(xts)
library(TTR)
data(ttrc) ## 仮想の企業 ttrc社 の株価データ
subdata<-ttrc[3001:3150,1:6]
#datasetのうち3001番目から150個のサンプル抽出
y<-as.xts(subdata)
ny<-length(y)
### 仮想の企業 ttrc社 の 終値 1996/11/12-1997/06/17 日次 終値
# daily closing 1996/11/12-1997/06/17 サンプル数 150
idx<-index(y)
### 感覚的に円で考えると安く見えるので100倍にしてみた。
y<-y[,"Close"]*100
plot(y,cex.axis=0.6,cex.main=0.6,main="株価と50日移動平均",
main.timespan=F)
lines(SMA(y, n = 50), on = 1, col = "red",lwd=2)
addLegend("topleft", on = 1,
legend.names = c("株価", "50日移動平均"),
lty = c(1, 1), lwd = c(2,2),
col = c("blue", "red"),cex=0.6)
###
##### SSModel のy は数値ベクトルにしておく。warning回避のため。
model5<-SSModel(as.vector(y) ~ SSMtrend(degree=2,Q =
list(matrix(NA), matrix(NA))),
H=matrix(NA))
fitmodel5<-fitSSM(model5,inits =
c(0,0,0),method="BFGS")
fitmodel5$model["H"] ### 観測誤差の分散 の推定値
### 観測誤差の分散
fitmodel5$model$H
fitmodel5$model$Q ##状態誤差の分散の推定値
## 水準の変動(1,1) トレンドの変動(2,2)
fitmodel5$model["Q"][1,1,1] ## 水準の誤差項の分散の推定値
fitmodel5$model["Q"][2,2,1] ## slopeの誤差項の分散の推定値
trendmodel5 <-
KFS(fitmodel5$model,filtering=c("state","mean"))
##################### カルマン平滑化推定値
#####################
#### 切片level 抽出
levelsmth<-trendmodel5$alphahat[,"level"]
levelsmth<-cbind(as.xts(idx),as.vector(levelsmth))
head(levelsmth)
class(levelsmth)
plot(levelsmth,ylab="level", main="カルマン平滑化 level",
main.timespan=F,
xlab="",cex.axis=0.6,cex.main=0.6)
lines(SMA(y, n = 50), on = 1, col =
"red",lwd=2,lty=1)
addLegend("topleft", on = 1,
legend.names = c("level","50日移動平均株価"),
lty = c(1,1), lwd = c(2,2),cex=0.8,
col = c("blue", "red"))
##### slope
###### slope の抽出
slopesmth<-trendmodel5$alphahat[,"slope"]
slopesmth<-cbind(as.xts(idx),as.vector(slopesmth))
plot(slopesmth,xlab="",type="l",
main.timespan=F,
cex.axis=0.6,cex.main=0.6,ylab="",
main="smoothed slope")
addLegend("topleft", on = 1,
legend.names = c("smoothed slope"),
lty =1, lwd = 2,cex=0.8,
col = "blue")
##### slope の累積和=trend
trendsmth<-cumsum(trendmodel5$alphahat[,"slope"])
trendsmth<-cbind(as.xts(idx),as.vector(trendsmth))
plot(trendsmth,xlab="",cex.axis=0.6,cex.main=0.5,
main="smoothed trend(slopeの累積和)",
main.timespan=F,ces.main=0.6,
ylab="trend")
######トレンドを含まないlevel
purelevel<-levelsmth-trendsmth
plot(purelevel,xlab="",cex.axis=0.6,cex.main=0.6,
main.timespan=F,
main="トレンドを含まない純粋level",ylab="pure level")
lines(y, on = 1, col = "red",lwd=2,type="l")
addLegend("bottomleft", on = 1,
legend.names = c("pure level", "株価"),
lty = c(1, 1), lwd = c(2,2),
col = c("blue", "red"))
################ filtered estimete att
############### att フィルター化 filtered estimate
#### levelの抽出 フィルター化
levelfiltatt<-trendmodel5$att[,"level"]
####
levelfiltatt<-cbind(as.xts(idx),as.vector(levelfiltatt))
plot(levelfiltatt,ylab="level",xlab="",
cex.axis=0.6,cex.main=0.6,col="red",lty=3,lwd=2,
main.timespan=F,
main="フィルター化levelの推移")
lines(y, on = 1, col = "blue",lwd=2,lty=3)
addLegend("topleft", on = 1,
legend.names = c("filtered level", "株価"),
lty = c(3, 3), lwd = c(2,2),
col = c( "red","blue"),cex=0.6)
#### slope の抽出 フィルター化
slopefiltatt<-trendmodel5$att[,"slope"]
####
slopefiltatt<-cbind(as.xts(idx),as.vector(slopefiltatt))
plot(slopefiltatt,ylab="slope",xlab="",
cex.axis=0.6,cex.main=0.6,col="blue",ity=1,lwd=2,
main.timespan=F,main="フィルター化 slopeの推移")
addLegend("topright", on = 1,
legend.names = c("filtered slope"),
lty = 1, lwd = 2,
col = "blue",cex=0.6)
##### slope の累積和=trend
trendfiltatt<-cumsum(trendmodel5$att[,"slope"])
trendfiltatt<-cbind(as.xts(idx),as.vector(trendfiltatt))
plot(trendfiltatt,xlab="",main.timespan=F,
cex.axis=0.6,cex.main=0.6,col="blue",ity=3,lwd=2,
main="slopeの累積和=トレンド",ylab="trend")
addLegend("topleft", on = 1,
legend.names = c("slopeの累積和=トレンド"),
lty = 1, lwd = 2,
col = "blue",cex=0.6)
######トレンドを含まないlevel
purelevelfiltatt<-levelfiltatt-trendfiltatt
plot(purelevelfiltatt,xlab="",ylab="",
main.timespan=F,
cex.axis=0.6,cex.main=0.6,col="blue",ity=3,lwd=2,
main="フィルター化 level(トレンド除外)")
lines(y, on = 1, col = "cyan",lwd=2,lty=1)
addLegend("bottomleft", on = 1,
legend.names = c("トレンドを除外したlevel","株価"),
lty = c(1,1), lwd = c(2,2),
col = c("blue","cyan"),cex=0.6)
##カルマンフィルターの1期先の予測値
#サンプルデータ数は150,one-step ahead は151番目
trendmodel5$a[,"level"][151]
## 150日目の時価は2581
y[150]
predy<- predict(trendmodel5$model, states =
"all",level=0.95,
interval = "confidence", filtered =T)
Fpredy<- predict(trendmodel5$model, states =
"all",n.ahead=10,level=0.95,
interval = "prediction", filtered =T)
### predy[,1] と fitted(trendmodel5,filtered=T) は同一内容
predy[,1]-fitted(trendmodel5,filtered=T)
predy[1:3,1]<-NA # 最初の3個はグラフ表示をスキップ
xpredy<-as.xts(predy)
xFpredy<-as.xts(Fpredy)
xFpredy[,1]
xs<-length(xpredy)
cbplot<-ts.union(c(xpredy,xFpredy))
head(cbplot)
cbplot
# cbplot<-ts(cbplot,start=c(1871),frequency=1)
matplot(cbplot,type="l",lwd=2,main="フィルター化推定値 と
その予測値",
xlab="",
ylab="株価",cex.main=0.7,xaxt="n")
matlines(y,lty=1,col="grey",lwd=2)
abline(v=151,col="purple",lwd=3,lty=3)
text(150,2800,"予測期間",cex=0.8)
rect(151,0,170,2900,col="green",density=100)
legend("topleft",
leg = c("95%信頼区間上限","フィルター化推定値",
"95%信頼区間下限","実績値"),
cex = 0.3, lty = c(2,1,3,1),
col = c("green", "blue","red","grey"),
lwd=c(2,2,2,2) )
name =
c("マーカー部分は1996-11-12から1997-06-17の150日間後のfiltered
estimate の予測値")
axis(1,at=80,labels=name,cex.axis=0.7)
参考文献
1.ブロックウェル/ デービス 著
逸見功,田中稔,宇佐美嘉弘,渡辺則生 訳
(2004)入門時系列解析と予測(改訂第2版)
シーエーピー出版株式会社(Brockwell and Davis Introduction to time series and
forecasting Springer-Verlag)
2. cran.rproject.org/web/packages/KFAS/
vignettes/KFAS: Exponential Family State Space Models in R Jouni
Helske
3.三中信宏 再現可能性ははたして必要なのか: p 値問題から垣間見る科学研究の多様性 計量生物学Vol.
38, No. 2, 117–125 (2017)
4.John C Hull(2003) Options, Futures, and Other
Derivatives, Prentice Hall
財務データ・サイエンティストの役割、 財務データの会計的分析と統計的分析の違い、状態空間モデルの応用など