カルマンフィルターの簡単な計算例を探究 with Excel and R
simple numerical examples of Kalman filtering and
smoothing using
Excel and R .
時系列分析ソフトを使っているとカルマンフィルターのアルゴリズムが内蔵されていてフィルター化された推定値などが出力されることが多い。どのようなアルゴリズムか知らなくても実務的には困ることは少ないかもしれないが、全くのブラックボックスというのも落ち着きが悪い。そこでカルマンフィルターの入門の入り口辺りを探ってみることにした。
例え話について
カルマンフィルター関連の入門的文献を読んでみるとロケットの動きとか工学的な現象によるたとえ話が多く出てくる。物理に強い人にとってはわかりやすいのかもしれないが、物理や工学に疎い人にはたとえ話を理解することすら難しい。個人的には、適切かどうかはわからないが不動産売買のたとえ話がわかりやすいように思う。ある人が実際に売却する予定はないが、もし自分の家屋を売却するとしたらどの程度の価格になるか密かに推定したいと考えた。当初の予想値として控えめに見積もって200と考えた。(単位は百万円でもドルでも好みで読まれたい)不動産情報を収集したところ、類似物件が1120で売れたという情報を得た。そこで、これは自分の予想値よりも高いので予想値を修正することにした。どのような修正をしたかというと
当初の予想値+K×(観測値-当初の予想値)
で求めることにした。Kは調整係数になるが、例えばK=0.5 として計算すると
200+0.5*(1120-200)=660
改訂後の予想値は660となった。別の新しい情報が入手できた。類似物件が1160で売れたようだ。そこで再び、この情報を織り込んで新しい予想値を同様の手法で計算した。660+0.5*(1160-660)=910
このようにして新しい観測値が入手される毎に予測値を逐次計算して更新していくのがカルマンフィルターの大雑把な考え方となっている。上記の例では調整係数 Kを0.5に固定していたが、カルマンフィルターでは後述するように観測値を入手する毎に推定値の分散等も考慮しながらK(カルマンゲイン
Kalman gain と呼ばれる)を更新する工夫が施されている。
カルマンゲイン(Kalman gain)と最小分散推定量について
確率変数x1とx2が独立のとき、ax1+bx2の分散は
V(ax1+bx2)=a2V(x1)+b2V(x2)となる。この関係を使って
(1-K)x1 +Kx2の分散を求めると上式から
V(x1,x2)=(1-K)2V(x1)+K2V(x2) を得る。
V(x1,x2)が最小になるようなKは V(x1,x2)をKで微分して求めると
K=V(x1)/(V(x1)+V(x2))
カルマンフィルターではKをカルマン・ゲイン(Kalman gain)と呼んでいる。Kは推定値の平均二乗誤差(MSE mean square error)を最小にするのでカルマンフィルターは最小分散推定量の性質を持っている。フリーの数学ソフトMAXIMAを使ってKの性質をもう少し調べてみる。独立の確率変数x1とx2の線形結合により得られた確率変数の分散は以下のように計算される。この分散が最小になるようなKを求めている。
このKを線形結合された確率変数の分散、Var(K)の式に代入すると
x1とx2を結合させた確率変数の分散はV1*V2/(V1+V2)となることがわかる。
つぎに(1-K)*V1を調べてみると
(1-K)*V1は、x1とx2を結合させた確率変数の分散V1*V2/(V1+V2)と等しい。つまり(1-K)*V1の計算で新しく結合された推定値の分散が得られることがわかる。カルマンフィルターでは後に示すようにV1=Pt|t-1,V2=Ht としてこの関係式に従って、新しい分散に更新処理されている。
状態空間モデルとローカル・レベル・モデルについて
時系列分析の専門書などを読んでいると状態空間モデルという用語をよく見かける。(詳細は参考文献1など参照されたい。)これは統計的手法の一種で観測対象を直接に観測できない状態変数のシステムと観測値を測定する観測モデルに分離してモデリングしてパラメータを推定する手法となっている。状態空間モデルのうち、基本的でシンプルなモデルにローカルレベルモデル(local level model)がある。レベル(level)とは、たとえて言うならば単純回帰モデルY=ax+b の切片bに相当する。回帰分析の場合は分析対象期間を通して切片bは一定、つまりglobalに定数であるが、ローカルレベルモデルではこの切片が時間とともに変化する。いわばlocalな切片を状態変数として観測値yを説明するモデルになっている。
一般的な線形状態空間モデルは
で表現される。
状態空間モデルは、状態とよばれる観測されない潜在的な確率変数 (状態変数)α を使用して観測値 y を説明しようするとモデルである。 状態空間モデルでは、状態と観測値の 2 つの変数で構成され、t 時点で観測される観測値 yt は状態 αt から生成されるとされる。そして、状態 αt は、状態 αt-1 のみに依存して定まる。
ここで
として、一変量(univariate)のモデルに単純化すれば
で表現できる。
上式のうち
システムモデル(状態方程式state equation と呼ばれている。ここでαtは観測不能な状態変数(state variabl)でηはシステムノイズ(誤差項)
を表す。状態変数 αt は、状態変数 αt-1 と誤差項(システムノイズ)に依存するランダムウォーク過程に従っている。
は観測モデルを表し、状態変数αtと観測ノイズ(誤差項)
から成っている。これは観測方程式(measurement equation)とも呼ばれている。
システムノイズと観測ノイズは互いに独立で系列相関も無いとする。
ここで所有する不動産の価格を状態変数αとしてローカルレベルモデルを作り、観測値y(類似物件価格)からカルマンフィルターでαを計算してみる。本来は最尤法で推定するはずのパラメーターHt(観測ノイズの分散),Qt(システムノイズの分散)は既知と仮定している。
手順としては
で1期先を予測してからカルマンゲインを計算する。(V1=Pt|t-1,V2=HtとしK=V1/(V1+V2)の関係式が使われている。)
観測値を得ると予測値とその分散を更新する。(ここで前述した(1-K)*V1の関係式がV1=Pt|t-1,として使われている。)
で更新処理する。
この手続きを観測値を得る毎に逐次計算する。(数式の導出等は参考文献1.などを参照されたい)
カルマンフィルターによるフィルタリングの簡単な計算例
観測値として1120,1160,963,1210,1160, 1160,813,1230,1370,1140
の10個のデータを得たとしてt=1からt=2まで計算してみる。
状態変数αの初期値は200、その分散は10000と設定している。観測ノイズの分散 Ht=12000 ,システムノイズの分散 Qt=1300で時間的に不変と仮定している
時点ゼロにおける時点1の予測値は、状態変数の初期値をそのまま使用する。予測値の分散についてはQt=1300が加算される。
予測
時点1で観測値1120を得たのでカルマンゲインを計算し、予測値とその分散の更新をする。
更新
時点1における時点2の予測値とその分散を計算する。
時点2で新たな観測値1160を得たのでカルマンゲインを計算し、予測値その分散の更新をする。
更新
以下同様の逐次計算をする。
カルマンフィルターによるスムージング(平滑化)
フィルター化推定値を現時点から過去に遡って一定の算式で平滑化することをスムージングと呼んでいる。幾つかの方法があるが、その一つに固定区間スムージング(fixed interval smoothing)がある。固定区間スムージングでは
t= T-1,T-2,....2,1
の算式に基づき過去に向かって逐次計算(backward recursion)をする。数式だけ眺めても実感がわかないが、エクセルのシートを操作してみれば過去・現在・未来の観測値の影響を受けていることがわかる。RのパッケージKFASでは固定区間スムージングが使われている。(数式の導出等は参考文献1,2など参照)
フィルタリングは初期値に近い状態変数の推定値はバラツキが大きくなる傾向があるといわれているが、スムージングはより安定的であり事象の推定に向いているいわれている。
エクセルでカルマンフィルターの計算過程を探る(simple numerical examples of Kalman filtering and smoothing using Excel)
前述のフィルタリング計算例と同様の条件で10個の観測値を得たとしてフィルター化推定値等をエクセルで計算してみる。
価格データ(t=1から10)
(1120,1160,963,1210,1160, 1160,813,1230,1370,1140 )
状態変数αの初期値は200、その分散は10000と設定している。観測ノイズの分散 Ht=12000 ,システムノイズの分散 Qt=1300で時間的に不変と仮定している
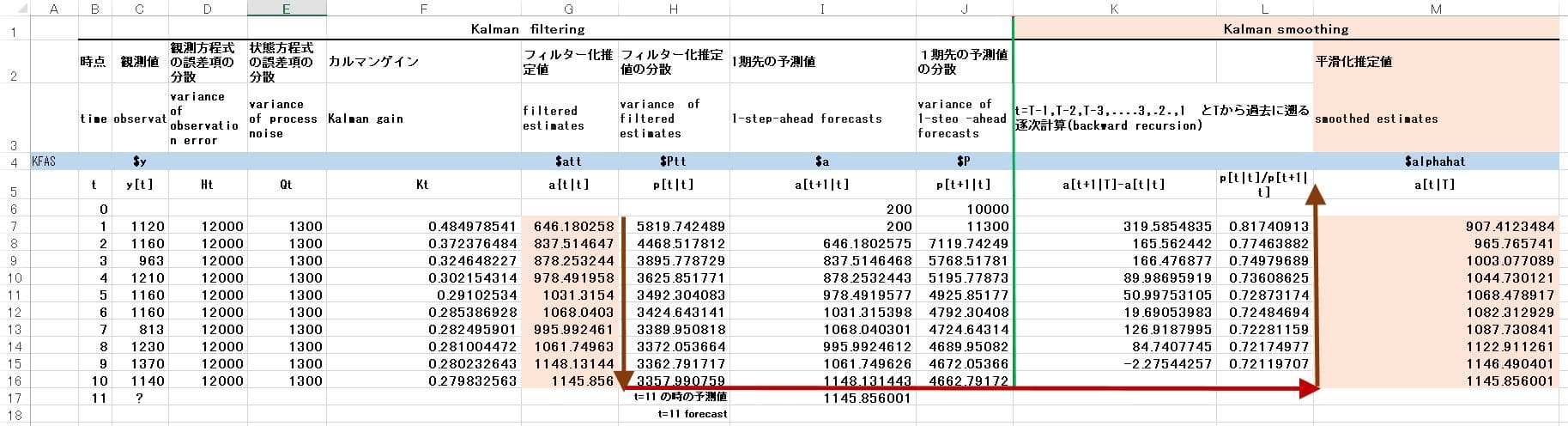
エクセルのシートに逐次計算の手順をまとめると以下のようになる。矢印が示すようにt=1からt=10と未来に向かって予測計算をしてフィルター化推定値を計算し、その後、向きを反転させてT=10からt=1まで過去に向かって(backward recursion)で平滑化推定値を固定区間平滑法で計算している。参考のためにRのパッケージKFASでoutputに使われている標記も薄青色マーカーの行で示している。
念のため、Excelの表のタイトルを縦方向に文字列で示すと
| 時点 | time |
| 観測値 | observation |
| 観測方程式の誤差項の分散 | variance of observation error |
| 状態方程式の誤差項の分散 | variance of process noise |
| カルマンゲイン | Kalman gain |
| フィルター化推定値 | filtered estimates |
| フィルター化推定値の分散 | variance of filtered estimates |
| 1期先の予測値 | 1-step-ahead forecasts |
| 1期先の予測値の分散 | variance of 1-steo -ahead forecasts |
| t=T-1,T-2,T-3,....3,.2.,1 とTから過去に遡る逐次計算(backward recursion) | |
| 平滑化推定値 | smoothed estimates |
Excelの表は以下のようになる。
数式表示で示せば
----------------------------
添付されたテキストファイルKalmanText.txtの利用法
このテキストファイルを開いて全てを選択し(空白部分も含めて)コピーしExcelの新しいシートの
セル番地A1にそのまま貼りつければ計算例のワークシートが再現できる。(Excel2016以降であれば可能、それより以前のversionではセルの分割作業が必要かもしれない)
具体的な手順は以下のとおり
1 このテキストファイルを開く
2 すべてテキストを選択する
3 Excelの新しいシートに貼りつける
To recreate the example worksheet, open this text
file, select everything (Ctrl + a), copy it, and paste it directly into cell
A1 of a new Excel sheet. (This is possible in Excel 2016 and later; earlier
versions may require splitting cells.)
The specific steps are as follows:
1. Open this text file.
2. Select all text (including blank spaces).
3. Paste it into cell A1 of a new Excel sheet.
ワークシートでなくテキストファイルを添付した理由などについてはエクセルのワークシートをテキスト化して簡単に通信
を御参照
----------------------------
RのパッケージKFASでカルマンフィルタ-(Kalman filtering and smoothing using KFAS(R package)
念のためにRのパッケージKFASのカルマンフィルターの関数KFSを使って計算してみる。ここではローカルレベルモデルのパラメータの推定が目的ではなくカルマンフィルターの計算過程を追跡するのが目的なのでfitSSMは使わずKFSだけで計算している。
KFASでは初期値をt=1で指定するようなのでa1=matrix(200,1,1),P1=matrix(11300,1,1)に設定してある。
library(KFAS)
## 初期値をエクセルに合わせる
y <-c(1120,1160,963,1210,1160, 1160,813,1230,1370,1140)
yM <- SSModel(y ~ SSMtrend(degree = 1,
Q = matrix(1300,1,1),
a1=matrix(200,1,1),P1=matrix(11300,1,1)),
H =matrix(12000,1,1))
# Kalman filtering
yKFS <- KFS(yM)
head(yKFS$model$y,20)
## [,1]
## [1,] 1120
## [2,] 1160
## [3,] 963
## [4,] 1210
## [5,] 1160
## [6,] 1160
## [7,] 813
## [8,] 1230
## [9,] 1370
## [10,] 1140
head(yKFS$att,20)
## level
## [1,] 646.1803
## [2,] 837.5146
## [3,] 878.2532
## [4,] 978.4920
## [5,] 1031.3154
## [6,] 1068.0403
## [7,] 995.9925
## [8,] 1061.7496
## [9,] 1148.1314
## [10,] 1145.8560head(yKFS$alphahat,20)
## level
## [1,] 907.4123
## [2,] 965.7657
## [3,] 1003.0771
## [4,] 1044.7301
## [5,] 1068.4789
## [6,] 1082.3129
## [7,] 1087.7308
## [8,] 1122.9113
## [9,] 1146.4904
## [10,] 1145.8560head(yKFS$a,20)
## level
## [1,] 200.0000
## [2,] 646.1803
## [3,] 837.5146
## [4,] 878.2532
## [5,] 978.4920
## [6,] 1031.3154
## [7,] 1068.0403
## [8,] 995.9925
## [9,] 1061.7496
## [10,] 1148.1314
## [11,] 1145.8560head(yKFS$P,20)
## , , 1
##
## [,1]
## [1,] 11300
##
## , , 2
##
## [,1]
## [1,] 7119.742
##
## , , 3
##
## [,1]
## [1,] 5768.518
##
## , , 4
##
## [,1]
## [1,] 5195.779
##
## , , 5
##
## [,1]
## [1,] 4925.852
##
## , , 6
##
## [,1]
## [1,] 4792.304
##
## , , 7
##
## [,1]
## [1,] 4724.643
##
## , , 8
##
## [,1]
## [1,] 4689.951
##
## , , 9
##
## [,1]
## [1,] 4672.054
##
## , , 10
##
## [,1]
## [1,] 4662.792
##
## , , 11
##
## [,1]
## [1,] 4657.991head(yKFS$Ptt,20)
## , , 1
##
## [,1]
## [1,] 5819.742
##
## , , 2
##
## [,1]
## [1,] 4468.518
##
## , , 3
##
## [,1]
## [1,] 3895.779
##
## , , 4
##
## [,1]
## [1,] 3625.852
##
## , , 5
##
## [,1]
## [1,] 3492.304
##
## , , 6
##
## [,1]
## [1,] 3424.643
##
## , , 7
##
## [,1]
## [1,] 3389.951
##
## , , 8
##
## [,1]
## [1,] 3372.054
##
## , , 9
##
## [,1]
## [1,] 3362.792
##
## , , 10
##
## [,1]
## [1,] 3357.991エクセルの計算と同じ推定結果を得た。
状態空間モデルを使って見えざる真の株価を状態変数として、過去、現在、未来を織り込んだ平滑化推定値を計算し、何か安定的な傾向を検出したり、あるいは平滑化推定値から大きく時価が乖離していれば平均回帰的な現象を予想することができるかもしれない。企業の見えざる正常利益を探ったり、会計監査で異常、不正(irregularities)を検知するためにも使えるかもしれない。尤もこのようなことはとうの昔から研究されているのだろう。
財務データ・サイエンティストの役割、 財務データの会計的分析と統計的分析の違い、状態空間モデルの応用など
時変AR1の状態空間モデルで株価分析
状態空間モデルをKFASとナイル川データで試してみる
日次の株価変動分析 ローカル・リニア・トレンド・モデルを使って株価予測
参考文献
1. ブロックウェル/ デービス 著
逸見功,田中稔,宇佐美嘉弘,渡辺則生 訳
(2004)入門時系列解析と予測(改訂第2版)
シーエーピー出版株式会社(Brockwell and Davis Introduction to time series and
forecasting Springer-Verlag)
2. cran.r-project.org/web/packages/KFAS/
vignettes/KFAS: Exponential Family State Space Models in R Jouni
Helske
3. www.kalmanfilter.net/JP/default_jp.aspx