時変AR1の状態空間モデルで株価分析 with KFAS　

　時変AR(1)モデル(time varying AR(1) modelについてパッケージKFASを使い、株価分析に有功かどうかを実験してみた。ブロックウエル、デーヴィスの訳書（参考文献1）ではARIMAモデルの状態空間表現が詳しく述べられているが、その中でも最もシンプルなAR(1)について時変AR1モデルを使って株価変動分析を行なった。適当な実際のデータが無かったのでやや乱高下気味の摸擬データを生成した事例と有名なBox,Jenkinsのテキストで使われていた1960年代のIBM株価について、時変AR1モデルを適用して実験してみた。

時変AR(1)モデル

時変AR(1)モデルの定義

観測方程式


状態方程式

なおｙは株価、Φ(t)は時変AR(1)係数、epsilon(t),eta(t)は誤差項（ホワイトノイズ）を表す。

乱高下気味の摸擬データの生成

set.seed(123) n <- 100 ar1 <- 0.5 # AR(1)係数 ar2<- 0.3 # AR(2)係数 sigma <- 0.2 # ノイズの標準偏差 # arima.sim でデータ生成 y1 <-round( (arima.sim(model = list(ar = c(0.5,0.3)), n = n, sd = sigma)+1)*100)

これをグラフで示すと

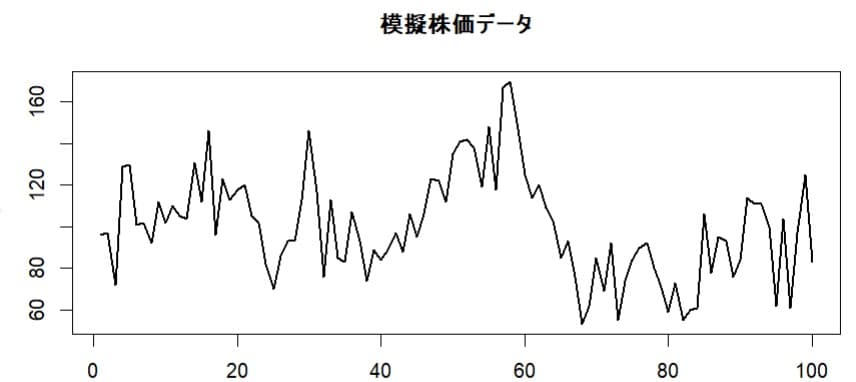
パッケージKFASを使い状態空間モデルを定義し時変係数の推定のためにupdate関数も作る。

Z <- matrix(y1[1:(n-1)], 1, n - 1) # y1{t-1}（遅延データ） # 時変AR1係数はランダムウォーク過程に従うとする。 tvmod <- SSModel(y1[2:n] ~ -1 + SSMcustom( Z = array(Z, dim = c(1, 1, n - 1)), T = matrix(1), R = matrix(1), Q = matrix(NA), P1 = matrix(0), P1inf = matrix(1) ), H = matrix(NA) ) # update関数 updatefn <- function(pars, model) { model$H[1,1,1] <- exp(pars[1]) model$Q[1,1,1] <- exp(pars[2]) return(model)

最尤法を使いパラメータの推定をしカルマンフィルターによる平滑化した時変AR(1)係数を推定する。

fittvmod <- fitSSM(tvmod, inits = c(0,0), updatefn = updatefn,method="Nelder-Mead") # カルマンフィルタで平滑化して 時変AR1を計算 resulttv <- KFS(fittvmod$model,filtering=c("state","mean")) resulttv$model$H resulttv$model$Q

観測誤差の分散は463.4005 、状態方程式の誤差の分散は1.700291e-10 と推定された。

平滑化した時変AR(1)係数の推移をグラフにすると次のようになる。

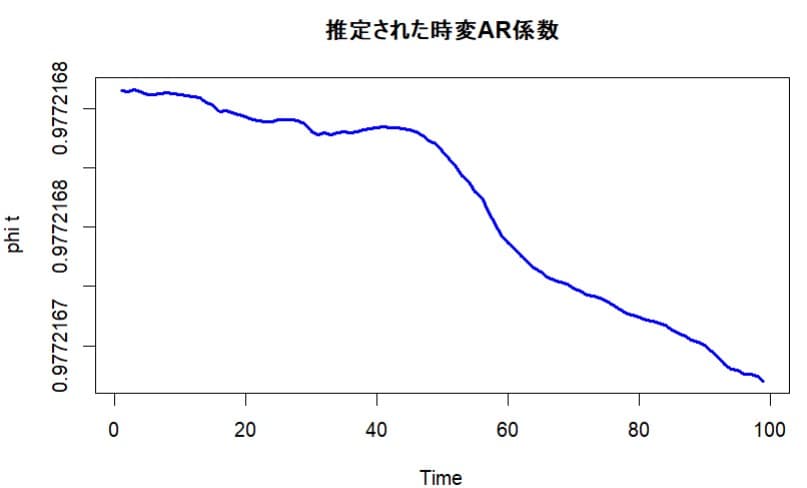
係数は0.977台であるが微小な低下傾向が見られる。

カルマンフィルター化推定値と平滑化推定値をグラフで表すと次のようになる。1期だけ遅行するので実績値を1期遅れて追いかける形になっている。

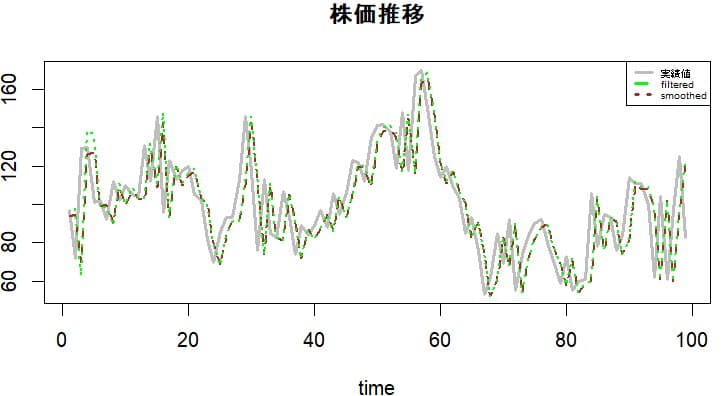
時変AR1係数は約0.98程度で安定しており株価はランダムウォーク過程に従っていることを裏付けているように思える。

カルマン平滑化推定値と実績値との残差を検討すると下記のようになる。

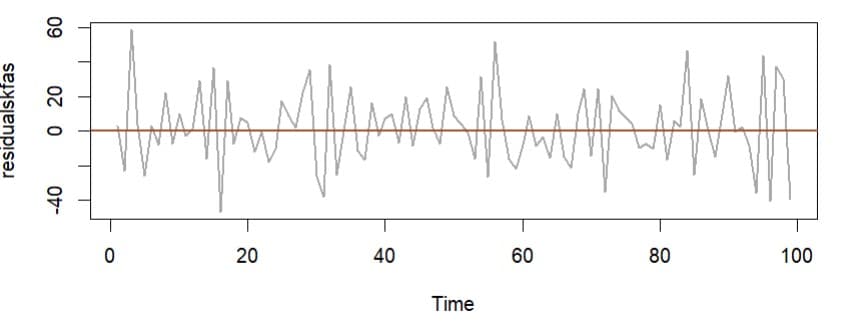
このコレログラムを調べると

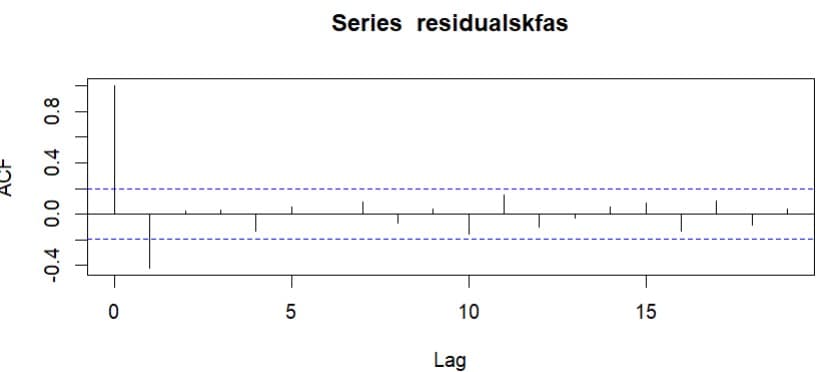
非定常過程の動きは追跡できているようだ。

1961年頃のIBMの株価を使って時変AR1モデルを適用

次にBox, G. E.P. and Jenkins, G. M. (1976) Time Series Analysis: Forecasting  and Control, HoldenDay, San Francisco, 2nd edition で使われている 1961/5/17から1962/11/2までのIBM 株価データに時変AR1モデルを適用してみる。パッケージ waveslim にIBM株価データが用意されているので,最初の100個のデータを使うことにする。

株価推移をグラフにすると次のようになる。

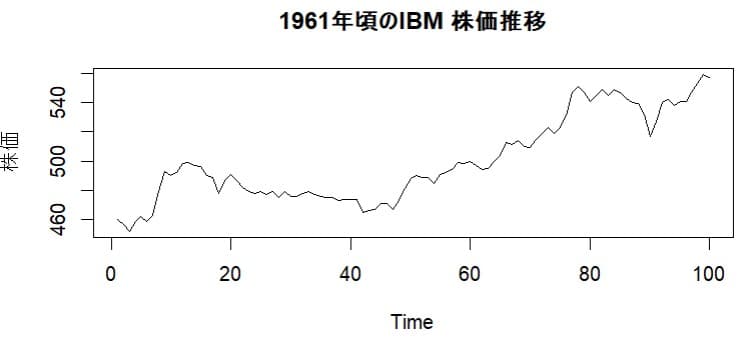
摸擬データの時と同じように時変AR1係数のカルマンフィルター化推定値をグラフにすると次のようになる。

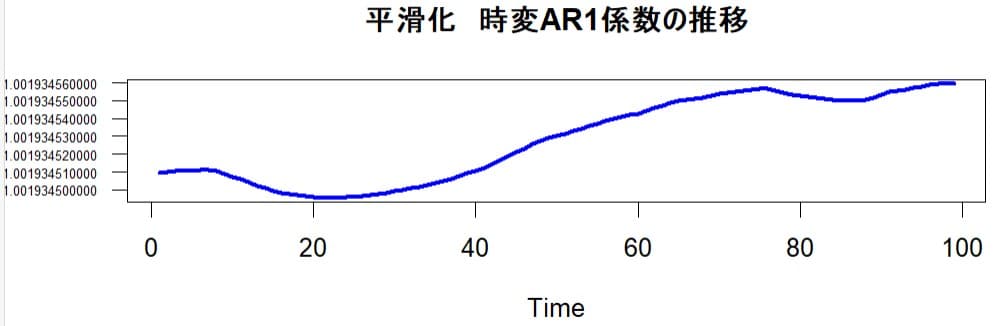
実質的には1に等しいが微小な範囲で変化していることが分る。

AR1係数の分布を調べると次のようになる。

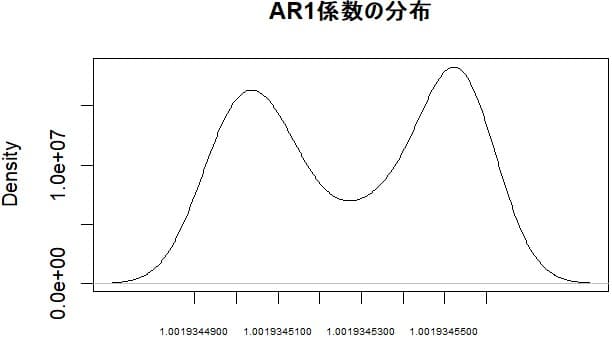
大変に微小な数値ではあるが山が2つできている。

時変AR1モデルでの株価予測と実績値をグラフにすると次のようになる。

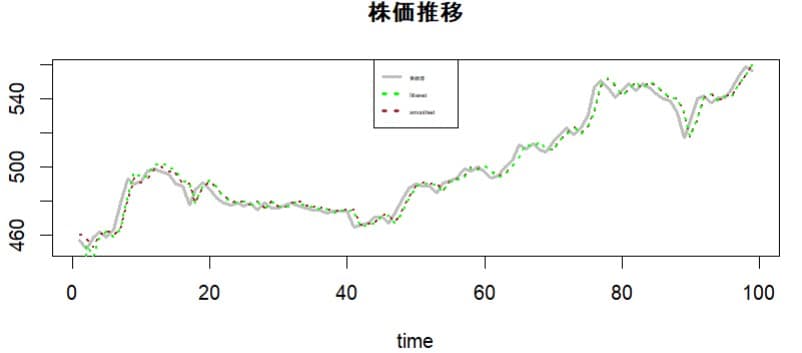
モデルの特性として実績値をベースにしたAR(1)係数に依存するため予測計算値は実績値の動きに1期遅行してしまう。しかし、実質的にAR(1)係数は1と見れるので株価のランダムウォーク仮説を支持するような結果となってしまった。短期的なトレンドが持続するような時期には何か株価動向のヒントが得られるかも知れない。

モデル予測値との残差とそのコレログラムも検討してみると

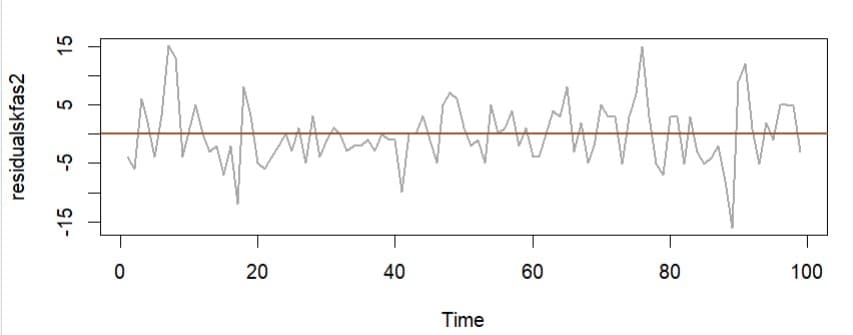
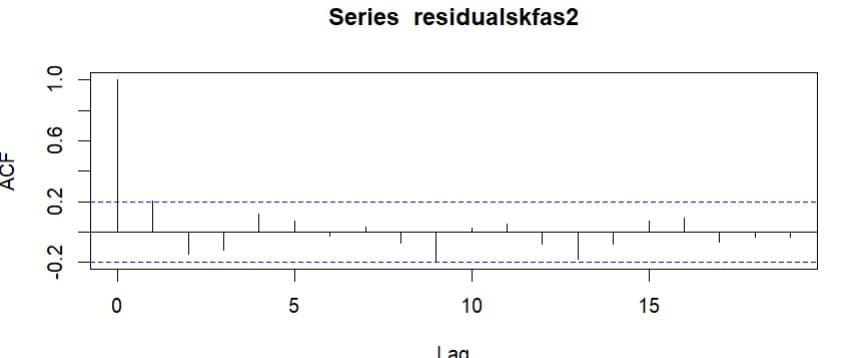
IBMの株価データについて単位根テストをすると予想通りに非定常と判定される。試しにパケージforecastを使いBoxJenkins法でAR(1)を適用すると単位根ありと判定されautoplotではグラフは作成されない。

　しかし、状態空間モデルを使えば差分データを作らずに原系列のまま非定常過程の動きを追跡できる。

時変AR1係数のカルマン平滑値の動向を注意深く分析することで何か強いトレンドが出ているかどうか等のヒントが得られるかもしれない。しかし、「もうはまだなり、まだはもうなり」 の相場格言通りに、その判断に悩むかもしれない。changepoint detection の基本的なアルゴリズムの勉強が必要かもしれない。

拙文を書くのに使ったRコードは以下のとおり。

library(KFAS)

##　乱高下気味の株価変動の模擬データを生成する

set.seed(123)
n <- 100
ar1 <- 0.5 # AR(1)係数
ar2<- 0.3 # AR(2)係数
sigma <- 0.2 # ノイズの標準偏差

# arima.sim でデータ生成
y1 <-round( (arima.sim(model = list(ar = c(0.5,0.3)),
n = n, sd = sigma)+1)*100)
ts.plot(y1, main = "模擬株価データ",lwd=2)


n<-length(y1)
n
## 状態空間モデルの定義
# 状態ベクトルは 時変AR1
Z <- matrix(y1[1:(n-1)], 1, n - 1) # y1{t-1}（遅延データ）

# 時変AR1係数はランダムウォーク過程に従うとする。
tvmod <- SSModel(y1[2:n] ~ -1 + SSMcustom(
Z = array(Z, dim = c(1, 1, n - 1)),
T = matrix(1),
R = matrix(1),
Q = matrix(NA),
P1 = matrix(0),
P1inf = matrix(1)
), H = matrix(NA) )

# update関数
updatefn <- function(pars, model) {
model$H[1,1,1] <- exp(pars[1])
model$Q[1,1,1] <- exp(pars[2])
return(model)
}

fittvmod <- fitSSM(tvmod, inits = c(0,0),
updatefn = updatefn,method="Nelder-Mead")


# カルマンフィルタで平滑化して 時変AR1を計算
resulttv <- KFS(fittvmod$model,filtering=c("state","mean"))

resulttv$model$H
resulttv$model$Q

resulttv$alphahat
# 時変AR係数の推定結果

plot.ts(resulttv$alphahat, type = "l", ylab ="phi t",
main = "推定された時変AR係数",col="blue",lwd=3)
length(y1)
length(y1[-1])
y1
y1[-1]
length(y1[-1])
length(fitted(resulttv))


plot.ts(y1[-1], ylab = "price", main = "株価推移",
xlab="time",col="grey",lwd=3)

lines(round(fitted(resulttv)),lty=2,col="brown",lwd=2)

fityf<-fitted(resulttv,filtered=TRUE)
fityf[1]<-NA
lines(round(fityf),lty=3,col="green",lwd=2)
legend("topright",
leg = c("実績値","filtered","smoothed"),
cex = 0.5, lty = c(1,2,3),col = c("grey", "green","brown"),
lwd=c(3,3,3) )

### このケースでは　フィルター化推定値と平滑化推定値はほとんど差異が無い


# 残差の計算
residualskfas <- residuals(resulttv, type = "response")


# 残差のプロット

plot.ts(residualskfas, col = "darkgrey", lty = 1,lwd=2)
abline(h = 0, col = "sienna",lwd=2)
## correlogram
acf(residualskfas)




### 1961年頃のIBMの株価を使って時変AR1モデルを適用してみる。

library(waveslim)
# Box, G. E.P. and Jenkins, G. M. (1976) Time Series Analysis: Forecasting
# and Control, HoldenDay, San Francisco, 2nd edition で使われている
# 1961/5/17から1962/11/2までのIBM 株価データを使うために、このパッケージを利用した。

data(ibm)

y2<-ts(head(ibm,100))

n<-length(y2)
n


plot.ts(y2,main="1961年頃のIBM 株価推移",ylab="株価")

# モデル定義
# 状態ベクトル　AR1
Z <- matrix(y2[1:(n-1)], 1, n - 1)

# 時変係数AR1はランダムウォーク
tvmod2 <- SSModel(y2[2:n] ~ -1 + SSMcustom(
Z = array(Z, dim = c(1, 1, n - 1)),
T = matrix(1),
R = matrix(1),
Q = matrix(NA),
P1 = matrix(0),
P1inf = matrix(1)
), H = matrix(NA) )

# update関数
updatefn <- function(pars, model) {
model$H[1,1,1] <- exp(pars[1])
model$Q[1,1,1] <- exp(pars[2])
return(model)
}

fittvmod2 <- fitSSM(tvmod2, inits = c(0,0), updatefn = updatefn,method="Nelder-Mead")


# 平滑化 時変AR1
resulttv2 <- KFS(fittvmod2$model,filtering=c("state","mean"))

resulttv2$model$H
resulttv2$model$Q


# 時変AR係数の推定結果
options(digits=12)
max(resulttv2$alphahat)
min(resulttv2$alphahat)
plot.ts(resulttv2$alphahat, type = "l",yaxt="n",ylab="",
main = "平滑化　時変AR1係数の推移",
col="blue",lwd=3)
axis(side=2, at=pretty(resulttv2$alphahat),
labels=formatC(pretty(resulttv2$alphahat),
digits=12,format="f"),las=1,
cex.axis=0.5)


plot(density(resulttv2$alphahat),xlab="",xaxt="n",main="AR1係数の分布")
axis(1, at = pretty(resulttv2$alphahat),
labels =format(pretty(resulttv2$alphahat),
nsmall=10,scientific=FALSE),cex.axis=0.5)


length(y2)
plot.ts(y2[-1], ylab = "price", main = "株価推移",
xlab="time",col="grey",lwd=3)

length(fitted(resulttv2))
lines(fitted(resulttv2),lty=3,col="brown",lwd=2)

fityf2<-fitted(resulttv2,filtered=TRUE)
length(fityf2)
lines(fityf2,lty=3,col="green",lwd=2)

legend("top",
leg = c("実績値","filtered","smoothed"),
cex = 0.3, lty = c(1,3,3),col = c("grey", "green","brown"),
lwd=c(3,3,3) )

### 単位根テスト
library(urca)

adftestur<-ur.df(y2,type=c("drift"))
summary(adftestur)
adftestur<-ur.df(y2,type=c("none"))
summary(adftestur)

# 残差の計算
residualskfas2 <- residuals(resulttv2, type = "response")


# 残差のプロット

plot.ts(residualskfas2, col = "darkgrey", lty = 1,lwd=2)
abline(h = 0, col = "sienna",lwd=2)
## correlogram
acf(residualskfas2)


#################### Box Jenkins
library(forecast)

arfit<-Arima(y2,order=c(1,0,0))
summary(arfit)
autoplot(arfit)