状態空間モデルをKFASとナイル川データで試す　playing with state space models using KFAS and Nile river data

playing with state space models using KFAS and Nile River Data

　状態空間モデルについては詳しく解説しているサイトが多数あるので学びやすい環境となっている。ここでは遊び感覚でパッケージKFASを使いながら簡単な状態空間表現を体得できるか実験してみた。

幸にも、入門的な統計学や計量経済学を学習する場合には高価な実験設備や試料等は不要で比較的に金銭をかけずに学習することが出来るよさがある。しかも統計ソフトRでは有名なテキストで使われているデータが装備されていることが多く大変に学習に便利である。統計ソフトRにはナイル川の水量データが標準で装備されており直ちに使えるので、これを使ってローカル・リニア・トレンド・モデルを試してみた。（Rコードは文末に掲載）

ローカル・リニア・トレンド・モデルl

行列によるモデル定義

ローカル・リニア・トレンド・モデルは下記のように観測方程式の他に2本の状態方程式で表現される。
観測方程式

状態方程式

なお

これらの方程式を行列で表現すると以下のようになる。

まず観測方程式を行列で表現すると

観測方程式は１行２列の行ベクトルに２行1列の列ベクトルを乗ずると当初の観測方程式

と同じ結果を得る。

状態方程式を行列で表すと

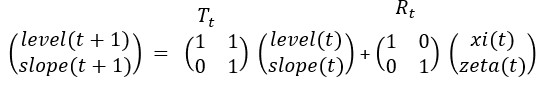
状態方程式　行列

行列演算をすれば下記のような元の方程式体系になる。

KFASでがマトリックスを使てモデルの定義をする。

観測方程式は

なので

Z=matrix(c(1,0),1,2)

と定義する。TやRも同様にして

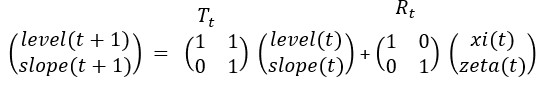
状態方程式　行列

から

T=matrix(c(1,0,1,1),2,2)

R=matrix(c(1,0,0,1),2,2)

と定義する。2本の状態方程式の誤差項の分散は２行2列の対角行列になるので

Q=matrix(c(NA,0,0,NA),2,2)

NAはこれから最尤法で推定することを表している。

H=matrix(NA) )　のNAも同様に観測方程式の誤差項の分散をこれから最尤法で推定することを示している。詳細はKFASのマニュアルに書かれている。

y01Tmodel<-SSModel(
y ~ -1 + SSMcustom(
Z=matrix(c(1,0),1,2),
T=matrix(c(1,0,1,1),2,2),
R=matrix(c(1,0,0,1),2,2),
Q=matrix(c(NA,0,0,NA),2,2),
P1inf=matrix(c(1,0,0,1),2,2),
),H=matrix(NA) )

と定義したモデルを最尤法を使って

fitLLMTy01<- fitSSM(inits = c(0,0,0) , model = y01Tmodel, method = "BFGS")
推定すると

観測方程式の誤差項epsilonの分散は

fitLLMTy01$model$H

で

         [,1]
[1,] 14673.27

を得る。

状態方程式の誤差項の分散行列は

fitLLMTy01$model$Q

で

         [,1]        [,2]
[1,] 1760.084 0.000000000
[2,]    0.000 0.004686483

を得る。

　状態方程式の1番目はlevelを表しているのでlevelの誤差項xiの分散は　1760.084　

状態方程式の２番目はスロープを示しているのでスロープの誤差項zetaの分散は　0.004686483　と小ことがわかる。

このモデルをカルマンフィルターによってフィルター化推定値(filtered estimate)と平滑化推定値(smoothed estimate)を計算してみる。

y01tKFS <- KFS(fitLLTM$model,filtering=c("state","mean"))

フィルター化推定値の最初の部分は

> head(y01TKFS$a)
       custom1    custom2
[1,]    0.0000   0.000000
[2,] 1120.0000   0.000000
[3,] 1200.0000  40.000000
[4,]  922.4813 -78.500006
[5,] 1136.3994   8.088516
[6,] 1164.0529  12.862666

平滑化推定値の最初の部分は

> head(y01TKFS$alphahat)
      custom1   custom2
[1,] 1120.797 -3.421958
[2,] 1117.470 -3.421958
[3,] 1109.042 -3.421945
[4,] 1118.132 -3.421966
[5,] 1116.203 -3.421990
[6,] 1109.020 -3.422004

列の名称にはcustom1,custom2 が付されているが状態方程式の定義の順番からcustom1 は level custom2 は　slopeを意味する。状態方程式1の定義

からlevelにはslopeが加算されているのでcustom1の数値にはcustom2の数値が加算されちることになる。何らかの理由でlevelだけの推移を見たい場合には別途に
custom1-custom2
を計算する必要がある。

custom1,custom2を使わずに好みの任意の名称を使いたい場合には

y02TmodelNew<-rename_states(y02Tmodel,c("レベル","傾き"))

と変えることが出来る。例えば、

y012TmodelNew<-rename_states(y01Tmodel,c("レベル","傾き"))

として

fitLLMTy012New<- fitSSM(inits = c(0,0,0) , model = y012TmodelNew, method = "BFGS")
y012TKFSNew <- KFS(fitLLMTy012New$model,filtering=c("state","mean"))

と改めて計算すると

 head(y012TKFSNew$a))
        レベル       傾き
[1,]    0.0000   0.000000
[2,] 1120.0000   0.000000
[3,] 1200.0000  40.000000
[4,]  922.4813 -78.500006
[5,] 1136.3994   8.088516
[6,] 1164.0529  12.862666
> head(y012TKFSNew$alphahat)
       レベル      傾き
[1,] 1120.797 -3.421958
[2,] 1117.470 -3.421958
[3,] 1109.042 -3.421945
[4,] 1118.132 -3.421966
[5,] 1116.203 -3.421990
[6,] 1109.020 -3.422004

列名変更後の出力を得る。

状態方程式の順番を変えた場合

つぎに状態方程式の1と2の順番を変えてみる。

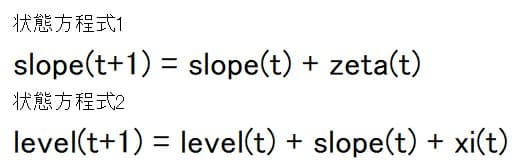
状態方程式2

この場合は行列表現が下記のように変わる。

まず、観測方程式はslopeとlevelの順番が変わるので下記のように表現される。

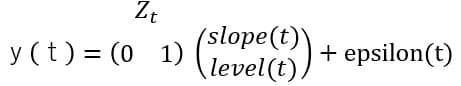
観測方程式　第2

従って、

Z=matrix(c(0,1),1,2)

状態方程式はマトリックス表現では

そこで

T=matrix(c(1,1,0,1),2,2)

R=matrix(c(1,0,0,1),2,2)

と定義し直す。

定義し直したモデル

y02Tmodel<-SSModel(
y ~ -1 + SSMcustom(
Z=matrix(c(0,1),1,2),
T=matrix(c(1,1,0,1),2,2),
R=matrix(c(1,0,0,1),2,2),
Q=matrix(c(NA,0,0,NA),2,2),
P1inf=matrix(c(1,0,0,1),2,2),
),H=matrix(NA) )

を最尤法で推定すると

fitLLMTy02<- fitSSM(inits = c(0,0,0) , model = y02Tmodel, method = "BFGS")

fitLLMTy02$model$H

14673.27

fitLLMTy02$model$Q

           [,1]     [,2]
[1,] 0.004686482    0.000
[2,] 0.000000000 1760.084

1行1列目には傾きの誤差の分散が出力され2行2列目にはレベルの誤差の分散が出力されている。更にカルマンフィルターによりフィルター化推定値と平滑化推定値を求めると

y02TKFS <- KFS(fitLLMTy02$model,filtering=c("state","mean"))

head(y02TKFS$a)
        custom1   custom2
[1,]   0.000000    0.0000
[2,]   0.000000 1120.0000
[3,]  40.000000 1200.0000
[4,] -78.500006  922.4813
[5,]   8.088516 1136.3994
[6,]  12.862666 1164.0529
> head(y02TKFS$alphahat)
       custom1  custom2
[1,] -3.421958 1120.797
[2,] -3.421958 1117.470
[3,] -3.421945 1109.042
[4,] -3.421966 1118.132
[5,] -3.421990 1116.203
[6,] -3.422004 1109.020

y01Tmodel のモデルの場合の

> head(y01TKFS$a)
       custom1    custom2
[1,]    0.0000   0.000000
[2,] 1120.0000   0.000000
[3,] 1200.0000  40.000000
[4,]  922.4813 -78.500006
[5,] 1136.3994   8.088516
[6,] 1164.0529  12.862666

　と較べるとcustom1とcustom2の内容が入れ替わっていることが分かる。

関数　SSMtrendを使ってモデルを定義

自由自在に行列を使って状態空間表現できる人にとってはSSMcustomでモデルの定義をするのが使い易いのだろう。しかし、そうでない場合はKFASでは幾つかの関数が用意されており詳細な行列表現をしなくても関数　SSMtrend を使うことでモデル定義が出来るようになっている。例えばSSMtrend でdegree=2 を指定するとlocal linear trend model が定義できる。

yLLTM <- SSModel(y ~ SSMtrend(degree = 2,
Q = list(matrix(NA),matrix(NA)) ), H = NA)
で状態空間モデルの定義をして、

fitLLTM<- fitSSM(inits = c(0,0,0) , model = yLLTM, method = "BFGS")

でパラメータを最尤法で推定すると

fitLLTM$model$H

14673.27

fitLLTM$model$Q

         [,1]        [,2]
[1,] 1760.084 0.000000000
[2,]    0.000 0.004686483

カルマンフィルターを使えば

ytKFS <- KFS(fitLLTM$model,filtering=c("state","mean"))

から

head(ytKFS$a)
         level      slope
[1,]    0.0000   0.000000
[2,] 1120.0000   0.000000
[3,] 1200.0000  40.000000
[4,]  922.4813 -78.500006
[5,] 1136.3994   8.088516
[6,] 1164.0529  12.862666
> head(ytKFS$alphahat)
        level     slope
[1,] 1120.797 -3.421958
[2,] 1117.470 -3.421958
[3,] 1109.042 -3.421945
[4,] 1118.132 -3.421966
[5,] 1116.203 -3.421990
[6,] 1109.020 -3.422004

今までの方法と同じ結果を得る。

ローカル・リニア・トレンドモデルのフィルター化推定値と平滑化推定値をグラフにしてみる。

plot.ts(y,col="grey",lwd=3,xlab="",main="フィルター化推定値と平滑化推定値")

lines(fitted(ytKFS),lty=1,col="brown",lwd=3)

yfiltered<-fitted(ytKFS,filtered=TRUE)

yfiltered[1]<-NA # yfiltered[1]にはゼロが入っているので
# (時点＝1)のグラフ表示をスキップさせる
lines(yfiltered,lty=1,col="cyan",lwd=3)

legend("top",
leg = c("y","filtered","smoothed"),
cex = 0.4, lty = c(1,1,1),col = c("grey", "cyan","brown"),
lwd=c(3,3,3) )

以下のようなグラフが描ける。

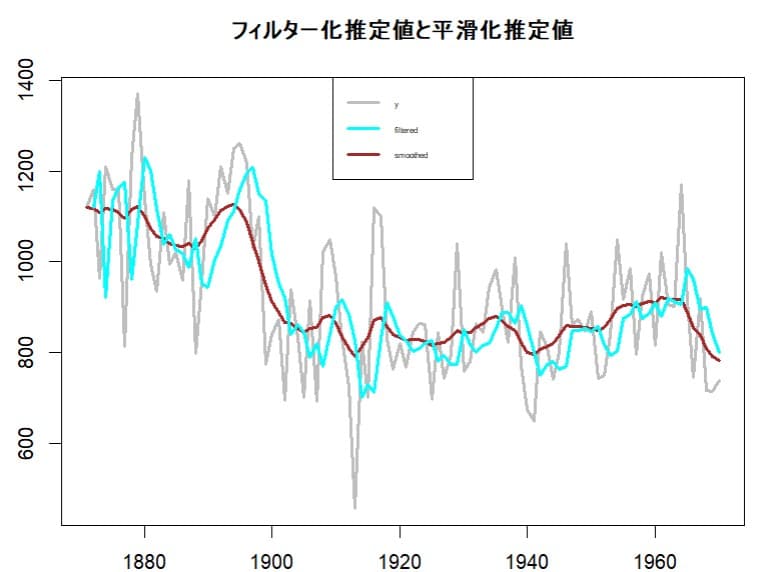
ローカルリニアトレンドモデル

関数　predict()を使って予測してみる

ローカル・リニア・トレンド・モデルの場合は関数predictを使いn.ahead=n でｎ期先の予測値を計算できる。作図の練習としてフィルター化推定値とその予測値をグラフにしてみる。

まず最初に10期先までの予測値を求める。

ypred <- predict(fitLLTM$model, n.ahead=10, interval="prediction",
filtered=TRUE)

######実績データと予測値データを結合
actuakforecast<-ts(c(yfiltered,ypred[,1]),start = 1871, frequency = 1)
actuakforecast[1]<-NA　　# actuakforecast[1]にはゼロが入っているので
# グラフ表示をスキップさせる
plot.ts(actuakforecast,ylab="水量",xlab="",
main="フィルター化推定値の推移と予測値",
col="cyan",lwd=2)
lines(ypred[,1], col = "red",lwd=3)

lines(y, col = "grey",lwd=2)
legend("top", legend = c("フィルター化推定値","実績値","将来予測値"),
col = c("cyan", "grey","red"),
lwd=c(2,2,2),lty = c(1,1,1),cex=0.3)

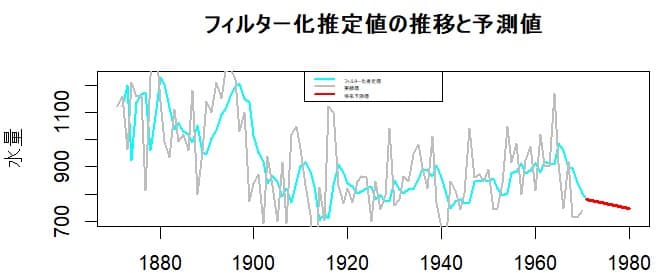
フィルター化推定値の推移と予測値

因みに、関数predict()を使って関数fitted()と同一の結果を抽出できる。まずpredict()でn.aheadの指定をはずしfiltered=TRUEの設定するとfitted(ytKFS,filtered=TRUE) と同一の内容が得られる。但し、 predict()の場合は信頼区間の上限、下限も出力されるので第1列目だけを抽出する。

ypred00 <- predict(fitLLTM$model, interval="prediction",
filtered=TRUE)
yfiltered<-fitted(ytKFS,filtered=TRUE)
#### ypred00[,1]-yfiltered を計算すると差異はゼロとなる。
ypred00[,1]-yfiltered

ypred00[,1]-yfiltered 　の差異がゼロとなり、両者が等しいことが分かる。

説明変数を使った回帰モデルのケース

ナイル川やアスワンダムの話しは小学校で学んで以来、特に学ぶ機会はなかったが今回少しだけ調べてみたが、イギリスにより1898年からナイル川を横切るダムAswan dam(Aswan low dam)の建設が開始され、1902年12月からその運用が始められたそうだ。多分その頃からナイル川の水量もコントロールされるようになったのだろうから 1902年以前と以降で水量が変化（shift)していると考えられる。そこでダミー(dummy)変数（intervention variableと呼ぶこともある）をモデルに取り入れてみた。計量経済学で消費水準が戦時下と平和時でどの様に変わるかを回帰分析するときにダミー変数を説明変数に加えるのと同じ手法である。

ダミー変数は1902年以前はゼロ、以降は1をとるようにセットしてある。

intervention <- rep(0, n)
intervention[which(time(y) >= 1902)] <- 1 # 1902年　以降は1にセットしてある。interventionは長い単語になるので

x<-intervention

としてｘで表示することにする。

この説明変数をlevelに加えると回帰モデルになる。

観測方程式は

状態方程式は

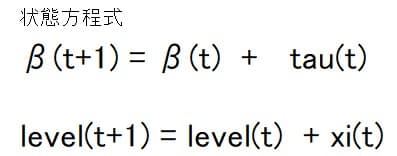
回帰モデル　状態方程式

なお、

これら方程式を行列で表現すると

観測方程式は

状態方程式は

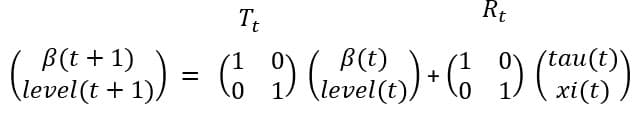
状態方程式　行列

で表現される。

最初に観測方程式をKFASで定義してみる。

からZt は配列

Zt<-array(dim=c(1,2,length(y)))

とする。配列は、1行2列のワークシートがｙのデータ数だけ積み騰がったｎ階建ての高層ビルのようなイメージとなる。

Zt[1,1,]<-x

として高層ビル1階からｎ階までに各階の1行1列目にｘを入れていく。

Zt[1,2,]<-1

で高層ビル1階からｎ階までに各階の1行2列目に1を入れていく。（通常の回帰分析で定数項のために1を使うのと同じ感覚）

状態方程式は

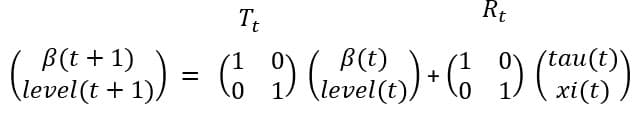
状態方程式　行列

であったから

T<-matrix(c(1,0,0,1),2,2)
R<-matrix(c(1,0,0,1),2,2)

と定義する。

Q<-matrix(c(NA,0,0,NA),2,2)

すると

regmod01 <- SSModel(
y ~ SSMcustom(Z = Zt, T =T, R=R,Q = Q,
P1=matrix(c(0,0,0,0),2,2),
P1inf=matrix(c(1,0,0,1),2,2)) ,
H = matrix(NA)
)

のようなモデルが定義できる。

これを最尤法で推定し

fitmod <- fitSSM(regmod01, inits = c(0,0,0), method = "BFGS")

から

fitmod$model$H

 18270.51

観測方程式の誤差項epsilonの分散は

18270.51

と推定されている。

fitmod$model$Q

        [,1]      [,2]
[1,] 0.3199321 0.0000000
[2,] 0.0000000 0.5439452

　を得る。

βの誤差項tauの分散は0.3199321

と推定されている。

levelの誤差項xiの分散は

0.5439452 　と推定されている。

回帰モデルを状態空間表現するのは面倒なのでKFASに用意されている関数　SSMtrend とSSMregression を使ってモデルを定義してみる。

regmod02<-SSModel(
y ~ SSMtrend(degree=1,Q=list(matrix(NA))) +
SSMregression(~ -1 + x,Q=matrix(NA)),H=matrix(NA)
)

これを最尤法で推定すると

fitmod02 <- fitSSM(regmod02, inits = c(0,0,0), method = "BFGS")

fitmod02$model$H

18270.51

fitmod02$model$

         [,1]      [,2]
[1,] 0.3199321 0.0000000
[2,] 0.0000000 0.5439452

同じ結果を得る。

ここから以降はこの回帰モデルregmod02の推定結果を使って話しをすすめてみる。

モデルregmod02をカルマンフィルターによってフィルター化推定値(filtered estimate)と平滑化推定値(smoothed estimate)を計算してみる。

フィルタリングとスムージングか関数KFSで計算する。

regmodkfs <- KFS(fitmod02$model,filtering=c("state","mean"))

一部の出力を見ると

フィルター化推定値は

head(regmodkfs$a)

   x    level
[1,] 0    0.000
[2,] 0 1120.000
[3,] 0 1140.000
[4,] 0 1080.997
[5,] 0 1113.251
[6,] 0 1122.603

xの列は回帰係数、levelの列はlevel の推定値となっている。

平滑化推定値は

head(regmodkfs$alphahat)

            x    level
[1,] -221.2017 1071.890
[2,] -221.2017 1071.888
[3,] -221.2017 1071.884
[4,] -221.2017 1071.883
[5,] -221.2017 1071.878
[6,] -221.2017 1071.871

同様に、xの列は回帰係数、levelの列はlevel の推定値となっている。

回帰モデルの予測値は
β*ｘ + level 　を計算する必要があるが関数fitted()を使って容易に計算できる。

　グラフにしてみるとダミー変数を付けくわえたことで水量の変化を捉えているように見える。

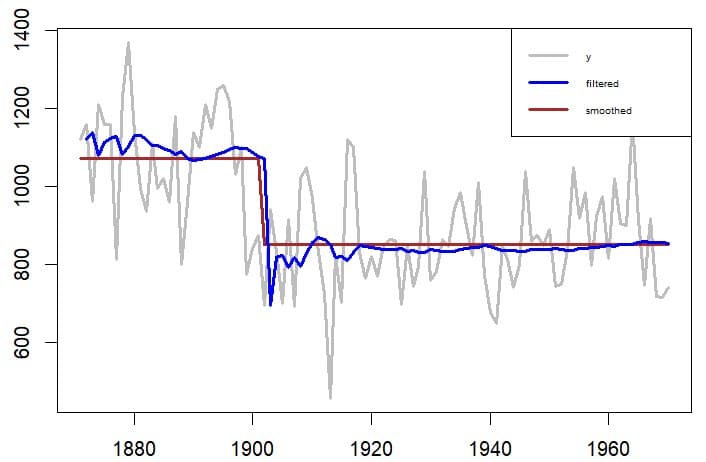
介在変数　回帰モデル

念のためにに関数fitted()が具体的にどの様な計算をしているのか確かめてみる。

(フィルター化推定値のケース)

regmodkfs$a は1期先までの予測値が含まれベクトルで長さも
n+1 と　ｘのベクトルの長さｎよりも1個多いので、
n1<-n+1 で
最後のn+1 番目のデータn1を除外して長さを揃える。

egmodkfs$a[,1][-n1]
長さを揃えたところで

β*ｘ + level

の計算をし、fitfilteredに格納する。

fitfiltered<-regmodkfs$a[,1][-n1]*x + regmodkfs$a[,2][-n1]

ここで

fitfiltered-fitted(regmodkfs,filtered=TRUE)

を計算すると差異がゼロとなり両者が等しいことが分かる。

(平滑化推定値のケース)

同様にして平滑化推定値のケースも

fitsmooth<-regmodkfs$alphahat[,1]*x + regmodkfs$alphahat[,2]
fitsmooth-fitted(regmodkfs)

差異がゼロになり両者は等しいことが分かる。

この回帰モデルはｘを市場ポートフォリオの超過収益率、ｙを個別銘柄の投資収益率のデータを当てはめればベータの時変回帰モデルに応用できる。

拙文を書くのに使ったRコードは以下のとおり。

library(KFAS)

data(Nile)

y <-Nile
n<-length(y)

##### 状態空間表現によるモデリング

### 行列による状態空間表現
## 状態方程式の行列表現（1）
# Z=matrix(c(1,0),1,2)
# T=matrix(c(1,0,1,1),2,2)

##### level、slope の順での状態空間表現

y01Tmodel<-SSModel(
y ~ -1 + SSMcustom(
Z=matrix(c(1,0),1,2),
T=matrix(c(1,0,1,1),2,2),
R=matrix(c(1,0,0,1),2,2),
Q=matrix(c(NA,0,0,NA),2,2),
P1inf=matrix(c(1,0,0,1),2,2),
),H=matrix(NA) )

fitLLMTy01<- fitSSM(inits = c(0,0,0) ,
model = y01Tmodel, method = "BFGS")

fitLLMTy01$model$H
fitLLMTy01$model$Q

y01TKFS <- KFS(fitLLMTy01$model,filtering=c("state","mean"))
head(y01TKFS$a)
head(y01TKFS$alphahat)

##### 状態名　custom1 custom2　は任意の名称に変更できる

y012TmodelNew<-rename_states(y01Tmodel,c("レベル","傾き"))
fitLLMTy012New<- fitSSM(inits = c(0,0,0) ,
model = y012TmodelNew, method = "BFGS")
y012TKFSNew <- KFS(fitLLMTy012New$model,filtering=c("state","mean"))
head(y012TKFSNew$a)
head(y012TKFSNew$alphahat)

##########################

### 行列による状態空間表現
## 状態方程式の行列表現（2）
# Z=matrix(c(0,1),1,2)
# T=matrix(c(1,1,0,1),2,2)

##### slope,level の順での状態空間表現

y02Tmodel<-SSModel(
y ~ -1 + SSMcustom(
Z=matrix(c(0,1),1,2),
T=matrix(c(1,1,0,1),2,2),
R=matrix(c(1,0,0,1),2,2),
Q=matrix(c(NA,0,0,NA),2,2),
P1inf=matrix(c(1,0,0,1),2,2),
),H=matrix(NA) )

fitLLMTy02<- fitSSM(inits = c(0,0,0) , model = y02Tmodel,
method = "BFGS")

fitLLMTy02$model$H
fitLLMTy02$model$Q

y02TKFS <- KFS(fitLLMTy02$model,filtering=c("state","mean"))
head(y02TKFS$a)
head(y02TKFS$alphahat)
## 状態方程式の行列表現（1）の場合と比較するとり
# 推定結果は同一であるが　custom1 custom2 の列の数値が入れかわり、
# Q の分散共分散行列も　行が入れかわっている。

##########################
##### local linear trend model by SSMtrend()

yLLTM <- SSModel(y ~ SSMtrend(degree = 2,
Q = list(matrix(NA),matrix(NA)) ), H = NA)

fitLLTM<- fitSSM(inits = c(0,0,0) , model = yLLTM, method = "BFGS")

fitLLTM$model$H
fitLLTM$model$Q

# run Kalman Filter and Smoother with estimated parameters
ytKFS <- KFS(fitLLTM$model,filtering=c("state","mean"))

head(ytKFS$a)
head(ytKFS$alphahat)

### フィルター化推定値と平滑化推定値のグラフ
plot.ts(y,col="grey",lwd=3,xlab="",main="フィルター化推定値と平滑化推定値")

lines(fitted(ytKFS),lty=1,col="brown",lwd=3)

## フィルター化

yfiltered<-fitted(ytKFS,filtered=TRUE)

yfiltered[1]<-NA # yfiltered[1]にはゼロが入っているので
# (時点＝1)のグラフ表示をスキップさせる
lines(yfiltered,lty=1,col="cyan",lwd=3)

legend("top",
leg = c("y","filtered","smoothed"),
cex = 0.4, lty = c(1,1,1),col = c("grey", "cyan","brown"),
lwd=c(3,3,3) )
###################
##### predict()を使って予測してみる

ypred <- predict(fitLLTM$model, n.ahead=10, interval="prediction",
filtered=TRUE)

######実績データと予測値データを結合
actuakforecast<-ts(c(yfiltered,ypred[,1]),start = 1871, frequency = 1)
actuakforecast[1]<-NA　　# actuakforecast[1]にはゼロが入っているので
# グラフ表示をスキップさせる
plot.ts(actuakforecast,ylab="水量",xlab="",
main="フィルター化推定値の推移と予測値",
col="cyan",lwd=2)
lines(ypred[,1], col = "red",lwd=3)

lines(y, col = "grey",lwd=2)
legend("top", legend = c("フィルター化推定値","実績値","将来予測値"),
col = c("cyan", "grey","red"),
lwd=c(2,2,2),lty = c(1,1,1),cex=0.3)

###predict()でn.aheadの指定をはずしfiltered=TRUEの設定すると
## fitted(ytKFS,filtered=TRUE) と同一の内容が得られる。但し、
## predict()の場合は信頼区間の上限、下限も出力されるので1列目
## を抽出する

ypred00 <- predict(fitLLTM$model, interval="prediction",
filtered=TRUE)
yfiltered<-fitted(ytKFS,filtered=TRUE)
#### ypred00[,1]-yfiltered を計算すると差異はゼロとなる。
ypred00[,1]-yfiltered

######################## intervention variable

y <-Nile
n<-length(y)
intervention <- rep(0, n)
intervention[which(time(y) >= 1902)] <- 1 # 1902年　以降は1にセット
x<-intervention

###################### SSMRegression #####

Zt<-array(dim=c(1,2,length(y)))
Zt[1,1,]<-x
Zt[1,2,]<-1
T<-matrix(c(1,0,0,1),2,2)
R<-matrix(c(1,0,0,1),2,2)
Q<-matrix(c(NA,0,0,NA),2,2)

regmod01 <- SSModel(
y ~ SSMcustom(Z = Zt, T =T, R=R,Q = Q,
P1=matrix(c(0,0,0,0),2,2),
P1inf=matrix(c(1,0,0,1),2,2)) ,
H = matrix(NA)
)

fitmod <- fitSSM(regmod01, inits = c(0,0,0), method = "BFGS")
fitmod$model$H
fitmod$model$Q

regmod02<-SSModel(
y ~ SSMtrend(degree=1,Q=list(matrix(NA))) +
SSMregression(~ -1 + x,Q=matrix(NA)),H=matrix(NA)
)

fitmod02 <- fitSSM(regmod02, inits = c(0,0,0), method = "BFGS")
fitmod02$model$H
fitmod02$model$Q

# フィルタリングとスムージング
regmodkfs <- KFS(fitmod02$model,filtering=c("state","mean"))

head(regmodkfs$a)
head(regmodkfs$alphahat)

# 平滑化された状態の抽出

plot.ts(y,col="grey",lwd=3,xlab="",main="介入変数による回帰モデル")

lines(fitted(regmodkfs),lty=1,col="brown",lwd=3)

## フィルター化

fityf<-fitted(regmodkfs,filtered=TRUE)

fityf[1]<-NA # fityf[1]にはゼロが入っているので
# fityf(時点＝1)のグラフ表示をスキップさせる
lines(fityf,lty=1,col="blue",lwd=3)

legend("topright",
leg = c("y","filtered","smoothed"),
cex = 0.5, lty = c(1,1,1),col = c("grey", "blue","brown"),
lwd=c(3,3,3) )

########## fitted() の検証　　
### 平滑化推定値のケース
fitsmooth<-regmodkfs$alphahat[,1]*x + regmodkfs$alphahat[,2]
fitsmooth-fitted(regmodkfs)
### fitsmooth と　fitted(regmodkfs)　は
# （　β*X + llevel ）　を計算しており、同一内容。

### フィルター化平滑化推定値のケース
## regmodkfs$a は　1期先までの数値が含まれベクトルの長さも
## n+1 と　1個多いので、最後のn+1 番目のデータを除外する
n1<-n+1

fitfiltered<-regmodkfs$a[,1][-n1]*x + regmodkfs$a[,2][-n1]

### fitfiltered と　fitted(regmodkfs,filtered=TRUE)　は
# （　β*X + llevel ）　を計算しており、同一内容。

fitfiltered-fitted(regmodkfs,filtered=TRUE)


	
		参考文献

		1.ブロックウェル/ デービス 著
		逸見功,田中稔,宇佐美嘉弘,渡辺則生 訳
		(2004)入門時系列解析と予測（改訂第２版）
		シーエーピー出版株式会社(Brockwell and Davis Introduction to time series and 
		forecasting Springer-Verlag)
	
		2.岩波データサイエンス刊行委員会編(2017)　岩波データサイエンス Vol.6 
		特集：時系列解析　岩波書店 
	
	3. 
	https://cran.r-project.org/web/packages/KFAS/index.html

	

	
	
	 
	


	日次の株価変動分析　ローカル・リニア・トレンド・モデルを使って株価予測、機械的予測の問題点など　 
 
 
	 
 
 



 
	
	
	 
	
	金融工学を初等数学で　目次

簡単な状態空間モデルをKFASとナイル川データで実験してみる

ローカル・リニア・トレンド・モデルl

行列によるモデル定義

状態方程式の順番を変えた場合

関数 SSMtrendを使ってモデルを定義

関数 predict()を使って予測してみる

説明変数を使った回帰モデルのケース

簡単な状態空間モデルをKFASとナイル川データで実験してみる　

関数　SSMtrendを使ってモデルを定義

関数　predict()を使って予測してみる