(貨幣の時間価値）
貨幣に時間価値があるために、投資分析においては現在価値計算が行われる。今現在受け取る１万円と１年後に受け取る１万円は価値が異なる。もし、今現在１万円を受け取れば、それを安全運用して銀行預金や１年満期の国債に投資すれば１年後には利息を得て１万円以上となる。安全資産の利子率を6％とすると、１年後の受け取る１０，６００円は現在受け取る１万円と同じ価値となる。言い換えると、１年後に受け取る１万円の現在価値は９，４３４円（=10000/1.06)に等しいことになる。貨幣に時間価値があることは歴史的に古くから知られていたようで、たとえば新約聖書マタイによる福音書２５-14のタラントンのたとえ話からも窺うことができる。このたとえ話の解釈については例えば神父さんや牧師さんなどに教えてもらうことにして、２０００年くらい前の一般庶民は既に貨幣の時間価値を認識していたと推測される。時間経過とともに生ずるキャッシュには発生時期でその経済価値が異なるため、すべてのキャッシュの流列を現在価値に換算して投資分析を行い採算性等の比較検討が行われる。
リース料の支払いはキャッシュフローのパターンが単純なのでキャッシュフローの現在価値計算の計算例として理解しやすい。
５年間のリースで毎年２２３９６円を年初に支払うとした場合の５年間のキャッシュフローの現在価値は割引率6％とした場合、以下のように計算される。
５年間について各年のキャッシフローの現在価値を合計すると１０００００円となる。Excelの財務関数PVを使っても計算できる。
----------------
財務関数PVについて
PV(利率、期間、定額支払,将来会、支払期日）
期初払は支払期日に１、期末払は０を指定する。
=PV(0.06,5,22396,0,1)
PV関数では将来価値をゼロに指定すると現在価値は
¥-100,001
といったマイナスで返ってくる 。
----------------
このキャッシュフローを算式で示すと
上記のように毎年のキャッシュフローが22396で確定している場合には、その現在価値 ｆ（r）を割引率 ｒ の関数で示せば
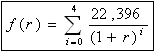
グラフで示せば
割引率（利子率）が大きくなれば現在価値は小さくなり、逆に、割引率が小さくなれば現在価値は大きくなる関係が読み取れる。
利子率を無限大に近づけると
現在価値は22,396へ収束する。
赤線で示すように、ｒ＝0.06 のところで ｆ（ｒ）＝100000 となっている。
リース料の支払いのようにキャッシュフローのパターンが単純な場合は現在価値を割引率の関係が単調減少関数で表現できる。しかし、投資プロジェクトのキャッシュフローで中途で大規模な修繕支出や事業廃止段階で環境原状回復の多額の支出が見込まれるような場合はキャッシュフロ－の符号がプラス、マイナスと時々に変化するので複雑な多項式になり凹凸のある曲線となるために内部利益率（IRR)も複数の解が見つかることがある。このような場合にはIRRの使用を避けて正味現在価値（NPV)を使うことが推奨されている。
上記のキャッシュフローの事例はリース料が年初払いであったが、リース料２２３９６が年末払いであったとすれば現在価値はどのように変化するだろうか。その他の条件に変更がないとしてキャッシュフローの現在価値を計算してみると以下のようになる。
５年間の現在価値合計は９４３４０円となる。各年のキャッシュの回収時点が１年遅れとなるため現在価値が低下している。
リース契約の借り手にとっては年末払いの方が有利なので年末払いで交渉したとすると、貸手にとっては不利のためリース料アップが提示されるだろう。どのようなリース料が提示されるか試算してみる。貸手にとって５年間のキャッシュフローの現在価値が１００，０００円を維持したいとすると下記のようになる。
毎年のリース料が２３７４０にすれば５年間キャッシュフローの現在価値は１００，０００円となる。Excelの財務関数PMTを使えば新リース料はPMT(0.06,5,100000,,0) で容易に求められる。詳細は資本回収係数を参照されたい。
一般的に言えば、現在価値を計算する場合には分子のキャッシュフローと分母に使う割引率が必要となる。割引率は貨幣の時間価値の換算（変換）目的であれば利子率が用いられるので
割引率＝利子率
となる。しかし、利子率といっても短期、中期、長期で利子率は異なってくるが、計算の便宜上、平均的な利子率を一つの割引率と考えて計算されている。この平均利子率は、債券のように毎年利金が入金し、満期には額面金額が流入するようなキャッシュフローの評価に使われる最終利回りの考え方と同様である。利回りの期間構造理論が示すように安全資産の利子率も残存期間が長くなればタームプレミアムも大きくなるので利子率も満期までの残存年数によって変化してくる。この利回りの期間構造を反映させた現在価値計算する場合には、残存年数に応じた割引債の利回りを割引率として使うことになる。さきほどの５年リースの例で言えば、分母の割引率は５年通して一定であったが、１年目の割引率は１年物割引債利回り、２年目は２年物割引債利回り・・・５年目は５年物割引債利回りといった具合になる。債券の時価評価をする場合には、このような計算が行われるが、計算が煩雑になるので通常のキャッシュフロー分析では一つの代表的な利子率が割引率として使われている。
つぎに分子のキャッシュフローに目を向けると、リース契約や貸付、債券投資のように毎期のキャッシュフローは契約不履行が無い限り確定しているような確実性の高いキャッシュフローもあれば、企業の利益やプロジェクト投資利益などの不確実性の高いキャッシュフローもある。不確実性の高いキャッシュフローを割り引き計算する場合には不確実性つまりリスクを織り込んだ資本コストが割引率として使われ
割引率＝資本コスト
となる。
キャッシュフローも株主に帰属するような残余利益を分子とするならば分母の資本コストは株主資本コストが使われ、
割引率＝株主資本コスト
となる。
分子が利子支払い前の利益であれば負債コストと株主資本コストの加重平均であるWACCが使われ
割引率＝WACC（加重平均資本コスト）
となる。
現在価値計算と言っても不確実性の高いキャッシュフローの見積の難しさに加えて、見積もられたキャッシュフローに適応する割引率を選択する必要があり、奥が深くなかなか一筋縄ではいかない。
資本コスト（cost of capital）と負債コスト、WACCとの関連性とCAPM