横軸に満期、縦軸に割引債の利回りをとり、満期毎の利回りをグラフにしたものをイールドカーブ(利回り曲線)といい、満期(満期までの残存期間)と利回りの関係を利回り期間構造と呼んでいる。利回り曲線は右上がり、水平、右下がりなど様々な形状になるが、その理由を説明する幾つかの仮説がある。その主なものを挙げてみる。
長期金利は、短期債券を再投資して運用した利回りに等しくなると仮定する。例えば5年物の割引債券を買って満期まで保有する場合と、5年間、毎年1年物の割引債券の買い入れ、償還金の再投資を繰り返すことで得られる利回りは裁定取引で等しくなる。下記の計算例で示すように、長期金利は将来の短期金利の期待値で決定される。フォワードレートが将来の短期金利の偏りのない期待値に等しいと仮定すれば長期金利は将来の短期金利の幾何平均に等しくなる。投資家が将来の短期金利が現在より高くなると予想すれば長期金利はそれを織り込んで金利は高くなり、グラフでは右上がりの曲線(順イールドと呼ぶ)となる。もし投資家が将来の短期金利が低下すると考えれば右下がりの逆イールドとなる。このように長期金利は将来の短期金利の期待値でのみ決定され、債券の満期までの残存年数は利回りに無関係と考える。純粋期待仮説はシンプルな仮説で将来の金利や債券価格の不確実性とそれに伴うリスクを全く考慮しないのでリスクプレミアムはゼロと仮定するので、長期金利は将来の短期金利の期待値で簡潔に表現できるメリットがある。しかし、逆に、この点が純粋期待仮説の弱点にもなっている。フォワードレートは将来の短期金利の偏りのない予測値を示すかどうかは議論が多いところだが、比較的に短時間の予測であれば、例えば実務的にはCMEグループのFEDの金利変更についての確率計算するFedWatchではフォワードレート(FF金利先物)が使われている。
金利変動などの債券投資リスクを考慮していないといった純粋期待仮説の弱点を補強しているのが流動性プレミアム仮説である。資金の運用期間が長くなれば将来の金利変動による損失リスクの可能性が大きくなる。満期前に売却する場合の価格は長期になるほど不確実性が高まるのでそれを補償するリスクプリミアムが必要となり長期金利は短期金利より高くなる。また資金の借り手は出来るだけ長期の安定した契約を好むが、貸し手は流動性の観点から短期を好むので貸し手の流動性を補償するプレミアムが必要となる。このような理由で満期までの残存年数が長くなればリスクプレミアムも大きくなる。この仮説によれば長期金利は将来の短期金利の期待値とリスクプレミアムの2つの要因で決定され、フォワードレートは将来の短期金利の期待値と流動性プレミアムが反映され、将来の短期金利の期待値だけでなくリスクプレミアムも加わったバイアスを含む短期金利の期待値となる。この仮説に従えば、例えば現時点でのフォワードレートで1年後の短期金利を予測するとリスクプレミアムが含まれているのでその分だけ過大に推定するのでバイアスのある予測値になる。流動性プレミアム仮説はバイアスのある期待仮説(biased expectations theory)として分類されることもある。利回り期間構造の実証分析では、将来の短期金利変動の不確実性や流動性低下に対するプレミアムをタームプレミアム(term premium)と呼び、長期金利は短期金利の期待値とタームプレミアムの合計から成ると考えて長期金利の変動を分析する研究が数多く行われている。この場合、タームプレミアムには金利リスクの他に流動性リスクや信用リスクなどのリスクプレミアムも含められている。年金基金のような長期投資家が長期債に投資して、低い金利でも利回りを長期にわたり固定したいと考えるような場合にタームプレミアムは圧縮される。地政学リスク等で極端なリスク回避が生じると特定の長期債に需要が集中して債券価格が異常に高くなるような時には、タームプレミアムがマイナスになることも起こりうる。
短期金利と長期金利は別々の市場で資金需給により決定されるという仮説である。債券市場の投資家は様々であるが、短期資金を調達して短期運用するような金融機関であれば資産負債を対応させ(マッチング)させるため短期債の投資に重点を置くだろう。仮に長期債投資が有利と考えられても長期債に投資することで資産負債の期日等のマッチングが出来なくなる部分が生じるリスクが生じるので、あえて長期債投資は避けるだろう。また金融機関によっては制度的あるいは内部管理的に運用規制があるかもしれない。年金ファンドのように長期運用する場合には長期債投資に専念すると考えられる。このようにしてイールドカーブは市場参加者のそれぞれの特性や制約条件により短期、中期、長期の満期区分の資金需給によって形成され、相互に独立して金利が決定されると主張する。
以上が利回り期間構造に係る主な仮説の概略であるが、利回り期間構造や金利モデルなどの理論では様々な利回り(レート rate)の用語が使われている。これら用語は実際に存在する概念であったり理論上の概念であったり、いろいろと混在している。 そこで試みに用語等を整理してみた。
スポットレート
ゼロレート(zero rate)とも呼ばれ、途中で利払いの無い、ゼロクーポン債(割引債)のレートのことを指す。割引債は満期に償還されるまで利払いが無いので中途の利金の再投資の利回りを考える必要が無いためシンプルな複利最終利回りとなる。このスポットレートを使って将来のキャッシュフローを現在価値に割り引いて債券価格(理論時価)が計算できる。利回り曲線は割引債の満期別の利回り(スポットレート)で表示されるが、現実に1年物割引債から50年物割引債まで連番で存在するようなものではなく理論上の考え方となる。
ショートレート
一定の短い期間(例えば1年、あるいは0.1秒など)の1単位期間に適用される利率をいう。単位を年で考えるとすれば1年物割引債スポットレートは1年間のショートレートと等しい。1年後の1年間のショートレート、2年後の1年間のショートレートも理論上は考えられるが現時点では未知であるが、やがて一定の時間が経過すればそのレートの実現値は判明する。ショートレートは現在も将来も含めた任意の時点で成立する短期金利といえる。スポットレートは割引債の最終利回りなので2年物、3年物、5年物といった複数期間のスポットレートが存在するがショートレートは1年のショートレート(1単位期間)だけである。理論的には、例えば3年物スポットレートは現時点での1年間のショートレート、1年後の1年間のショートレート、2年後の1年間のショートレートの幾何平均で表され、現時点でのショートレートは1年物スポットレートに等しい関係になる。 連続時間で考える利回り期間構造の数理モデルではショートレートは無限小の短期間に適用される金利を意味しており瞬間的ショートレート(instantaneous short rate)とも呼ばれている。連続複利で使われる金利は瞬間的ショートレートとなる。
フォワードレートは、将来のある時点からある時点までの一定期間の利回りのことであるが、現時点において考えられる将来の利回りである。例えば、現時点において1年後から2年後まで1年間資金を運用する場合に得られる利回りは、1年間のフォワード・レートである。2年物スポット・レートで2年間運用した時と、現在の1年物スポット・レートで1年間運用し、1年後から2年後までを1年間のフォワード・レートで運用したときの利回りは裁定取引により等しくなるはずなので、フォワード・レートはこの関係式で使って理論値を計算できる。これをインプライドフォワードレート(implied forward rate)と呼んでいる。
次のような割引債の利回りyが市場で成立していたとする。(期間単位は年とし、例えば、現時点は0、3年後満期のスポットレートはoy3 のように表示する)
| スポットレート y | ||
| 1年物割引債 | 0y1 | 0.05 |
| 2年物割引債 | 0y2 | 0.055 |
| 3年物割引債 | 0y3 | 0.06 |
タイムラインで示すと下図のようになる。
次の2つの投資案AとBを考える。裁定取引が行われれば均衡状態ではA案とB案の投資収益は等しくなるはずである。(n-1fn はn-1年からn年までの年間フォワードレートを表す)
(A) n-1年物割引債にn-1年間投資し、その後1年間 フォワードレート n-1fn で再投資して得る収益
(B) n年物割引債にn年間投資して満期に得る収益
フォワードレートはA=B となるようなブレーク・イーブンポイントのレートになっている。
図解すれば以下のようになる。
1年物割引債と2年物割引債との関係で見れば
| 1 + n-1fn =(1+0yn)n / (1+0yn-1)n-1 |
が成り立つ関係なので
| 1+1f2= | (1+0.055)2/(1+0.05) | ≒1.06 | |
| 1+2f3= | (1+0.06)3/(1+0.055)2 | ≒1.07 |
と計算できる。
見方を変えると、例えば3年物割引債のスポットレートは
{(1+0.05)*(1+0.06)*(1+0.07)}^(1/3)≒1.06
つまり3年物のスポットレートは3年間のフォワードレートの幾何平均となっている。(1年目のフォワードレートとスポットレートは等しい)
フォワードレートは将来のショートレートの期待値を示していると考えれば、 毎年のフォワードレートが上昇していればスポットレートも上昇するので利回り曲線は右上がりになる。もし毎年のフォワードレートが一定のままであればスポットレートも一定なので利回り曲線は水平になる。フォワードレートが下降していればスポットレートは右下がりになる。グラフで示せば
このように 純粋期待仮説によれば、フォワードレートが将来のショートレートの偏りのない期待値に等しいと仮定するので投資家が将来の短期金利が現在より高くなると予想すれば長期金利はそれを織り込んで右上がりになると主張する。投資家が将来の短期金利が下がると期待すれば利回り曲線は下降すると考える。利回り曲線は投資家の将来の短期金利の期待値で決定されるというシンプルな結論に至る。
流動性プレミアム仮説によれば、満期までの残存年数が長くなるリスクプレミアムが必要となる。仮にリスクプレミアムが1%必要だとすれば、1年物スポットレート5%、1年後、2年後のショートレートは5%と不変だとしても、リスクプレミアム分が1%上乗せされれば、1年後の1年物フォワードレート1f2 =6%(5%+1%)となり、2年物スポットレートは(1.05×1.06)1/2 -1=0.055で利回り曲線は右上がりになる。しかしショートレートは1年物も2年物も5%のまま不変で水平線である。フォワードレートはショートレートの期待値ではなくタームプレミアムが含まれて偏りのある期待値になっているのでスポットレートは右上がりになっている。下図参照。
上図は将来のショートレートやタームプレミアムが既知として作成されているが、実際のスポットレートなどのデータからタームプレミアムを推計するのは難しい課題となる。実証研究などでは利回り期間構造の数理モデルを使ってショートレートの期待値を推定する工夫が試みられているようだ。
年利6%で年に1回年末に利息を受け取れるとすれば1年後に(1+0.06)-1=6%の収益を得る。もし年に2回利息を受け取れ、それも再投資して複利運用できるならば1年後には(1+0.06/2)2-1=6.09%の収益を得る。もし毎日、再投資して複利運用できるとすれば(1+0.06/365)365-1=6.183%の収益となる。このようにして年利r%、複利運用回数mを無限大にした場合は1年後の収益は
となることが知られている。これを連続複利と呼んでいる。
年利5%で連続複利算
初期投資1円の5年後の元利合計 e0.05×5=e0.25 ≒1.284∙∙∙
5年後の1円の現在価値
1/e0.05×5=e-0.05×5=e-0.25≒0.778∙∙∙
何かの投資案件で連続複利ベースで1000円の初期投資が5年後には1284.03円回収できる予定であると説明された場合、連続複利ベースでの年間利益率は自然対数に変換して
ln(1.28403)/5=5% となる。
名目利率と連続複利の金利変換について
日常生活で通常に出会う複利計算と主に金融工学の世界で使われる連続複利計算を段階的に数値例でたどってみる。名目利率(年利)6%で1円を運用した場合の1年後の元利合計は1.06円になる。単純な話に見えるが結構に奥が深い。複利計算を半年ごとの行う場合には利息が半年ごとに元本に加算され半年ごとに複利計算が行われる。1年間に利息を元金に繰り入れる回数を転化回数と呼んでいるが、転化回数2の複利計算になり、1年後の元利合計は1.0609(1.03の2乗)で転化回数1の元利合計1.06より少し大きくなる。では毎月複利計算つまり転化回数12の複利計算での元利合計はどうなるか。元利合計は1.06168となりさらに少し大きくなる。この転化回数を限りなく大きくし、転化期間(利息繰り入れの期間)も限りなく小さくして 連続複利計算をすると1年後の元利合計は1.06184となる。つまり連続複利計算で名目利率6%を適用すると年間の実質利率は0.06184となる。もし実質利率を名目利率6%になるような利率を求めるならば0.0582689となる。(=log(1+0.06)=0.0582689)金融工学のテキストでは数式処理の便利さもあって連続複利がよく使われる。
実質利率(年利)i 、連続複利での利率 r で表すと
log(1+i)=r logは自然対数
の関係になる。言い換えれば
(1+i)=er
とも表せる。
i=0.06として前述の計算をまとめると以下のようになる。
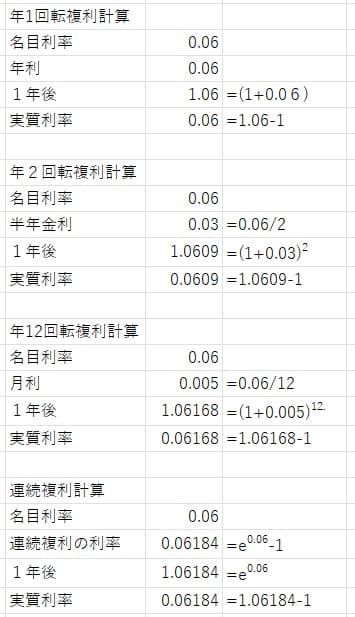
この連続複利の例で
(1+i)=er を使って確認すると
log(1+0.06184)=0.06
言い換えれば
1+0.06184 =e0.06の関係となる。名目利率6%をそのまま使って連続複利にすると実質利率は6.184%と少し大きくなる。
連続複利による純粋期待仮説
純粋期待仮説の妥当する世界でスポットレートとフォワードレートの関係を連続複利で見てみるとeの指数部分でフォワードレートの平均計算していることが分かる。例えば、3年物スポットレート(連続複利ベース)は
e((0.05+0.06+0.07)/3)=e0.06 からe0.06の自然対数をとるとln(e0.06)=0.06 と連続複利ベースでのスポットレートは0.06と計算できる。e0.06-1=1.06184-1=0.06184と計算すると年1回複利計算ベースでの実効スポットレートとなる。連続複利ベースで考える場合にはe0.06を自然対数に変換する。
前述の純粋期待仮説の設例でスポットレートとフォワードレートの関係を連続複利で計算してみると以下のようになる。
スポットレートがフォワードレートの平均値の形になっていることに注目すべきである。金利モデルを連続時間で理論的に考える場合には連続複利が使われる。
f(t,T)をt時点から任意の満期Tまでの期間のフォワードレートとして、現時点と満期までの時間を限りなく近づけ t ->T とした時のフォワードレートを瞬間的フォワードレートと呼ぶ。y(t,T)をt時点での満期Tまでのスポットレートとすれば、連続時間モデルでは
と表される。離散時間モデルと同様に、瞬間的フォワードレートを満期までの一定区間(t,T)で積分して、その期間数(T-t)で除して平均を計算している点は同じである。利回り期間構造モデルによる分析では、この関係性が応用されている。例えば、ネルソン-シ-ゲル(Nelson-Siegel)モデルではフォワードレートを定式化し、それを積分してスポットレート関数を導いている。
参考文献
John C Hull(2003) Options, Futures, and Other Derivatives, Prentice Hall
Frank J Fabozzi(1996) BOND MARKETS,ANALYSIS AND STRATEGIES 3rd ,Prentice Hall