退職後の資金について一定の利回りで運用しつつ、そこから一定の資金を引き出し、予定年数に到達したら残高がゼロとなるような定期取り崩し額を知りたい場合に資本回収係数が使われる。
当初の手元資金Pを利回りiで複利運用(年1回)しつつ毎年、定額のMを引き出しn年に達すると残高がゼロとなるような場合には
M=P×k となる資本回収係数 kが下記のような算式で求められる。
資本回収係数 k= i・(1+i)ⁿ/((1+i)ⁿ-1)
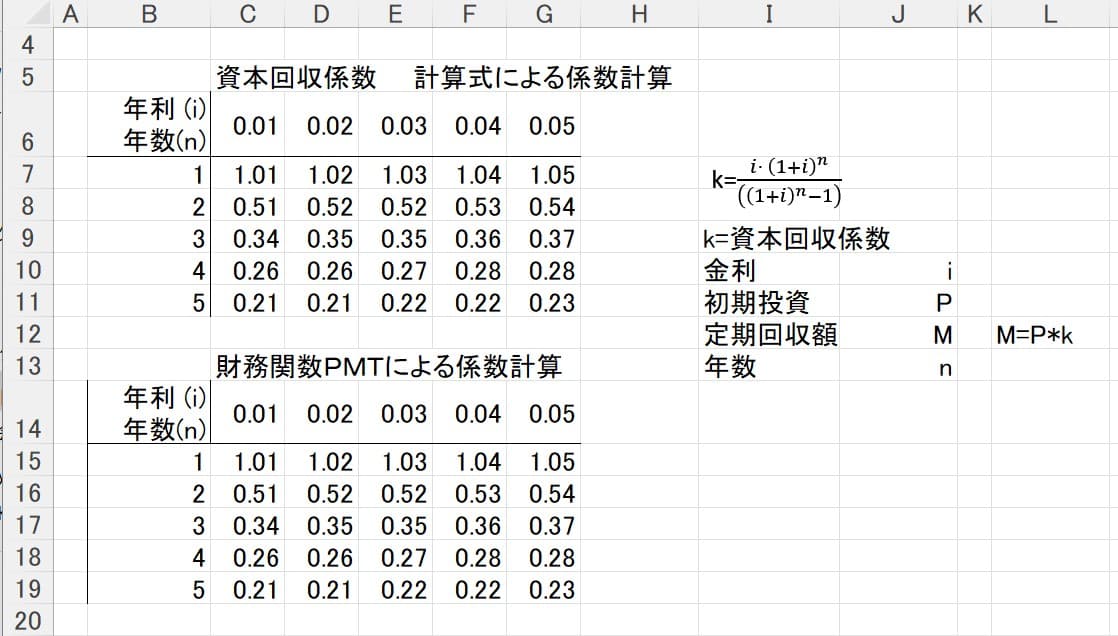
以下に示すように、エクセルで計算式を記入して求めてもよいし、エクセルの財務関数PMTを使って求めることもできる。年数と利回りによる係数表にしておくと使い勝手が良いので、その一例を作ってみた。

この表の計算式の一部を表示すれば下記のようになる。
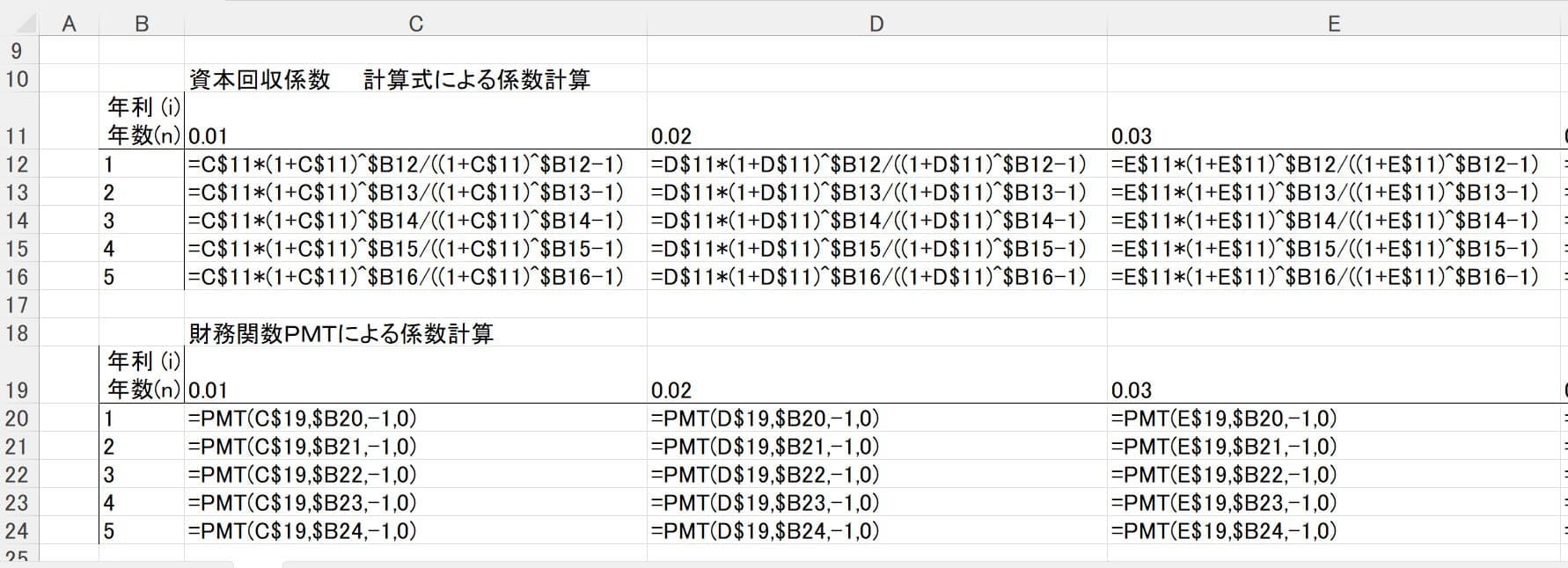
エクセルで 行と列の絶対参照を使い分け好みで金利の刻みを細かくしたり、年数を長くして自分用の係数表を作ることができる。しかし、通常は前述の算式を使うほうが速い。。
複利計算の回転数と資金引出の回転数が同じであれば、前述の算式
資本回収係数 k= i・(1+i)ⁿ/((1+i)ⁿ-1)
を応用できる。例えば、年利 i で半年毎の複利計算で、半年毎に資金を引き出す場合は r=i/2 T=n*2 として
資本回収係数 k= r・(1+r)T/((1+r)T-1)
と置き換えればよい。
もし、毎月の複利計算で、毎月の定額支払いであれば
r=i/12 T=n*12 とすればよい。
複利計算の回転数と支払い回数が異なるような変則的な場合、例えば、複利計算は年1回、支払い回数は年12回のようなケースでは前述の算式では対応できないので関数を自作するか何かの工夫が必要となる。これについては後述する。
ケース1
Aさんが定年になり退職金を1000万円受け取ったとする。今後20年間にわたって年利3%でこの資金を運用しつつ、しかも毎年一定額を生活費として取り崩し、20年後にはすべて資金を使い果たす計画を持っているとする。その場合にはAさんは毎年いくらを取り崩せるだろか。、資本回収係数の公式から
資本回収係数 k= i・(1+i)ⁿ/((1+i)ⁿ-1)
1000*0.03*(1+0.03)^20)/((1+0.03)^20-1) =67.2 月額では5.6万円となる。
ケース2
Aさんが定年になり退職金を1000万円受け取ったとする。今後20年間にわたって年利3%(ただし、毎月複利計算)でこの資金を運用しつつ、しかも毎月に一定額を生活費として取り崩し、20年後にはすべて資金を使い果たす計画を持っているとする。その場合にはAさんは毎月いくらを取り崩せるだろか。
これは、資本回収係数の公式から
資本回収係数 k= r・(1+r)T/((1+r)T-1)
r=i/12 T=n*12 として
計算すればよい。(1000*0.03/12*(1+0.03/12)^240)/((1+0.03/12)^240-1) =5.55 つまり年間で66万円となる。
ケース3 変則的な事例(複利計算のサイクルと支払いのサイクルが異なる場合)
Aさんが定年になり退職金を1000万円受け取ったとする。今後20年間にわたって年利3%(ただし、年間複利計算)でこの資金を運用しつつ、しかも毎月毎に一定額を生活費として取り崩し、20年後にはすべて資金を使い果たす計画を持っているとする。その場合にはAさんは毎月いくらを取り崩せるだろか。
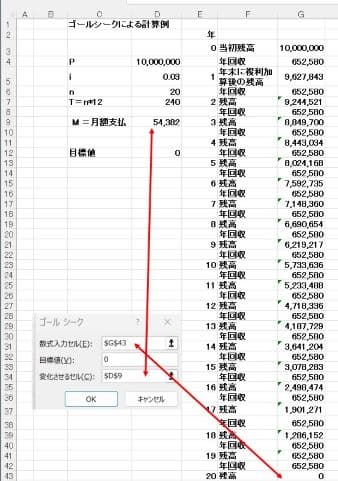
これは公式やエクセルのPMTでは計算できずVBAで関数を作るか、あるいエクセルで表を作りゴールシークで計算することになる。ここではゴールシークを使ってみると毎月の支払額は54.3千円、年額で65.2万円となる。どのケースも金利が3%ぐらいだと大きな差は生じないが金利が8%などと高くなると差異は大きくなる。
ゴールシークによる計算
ワークシートを数式表示させると
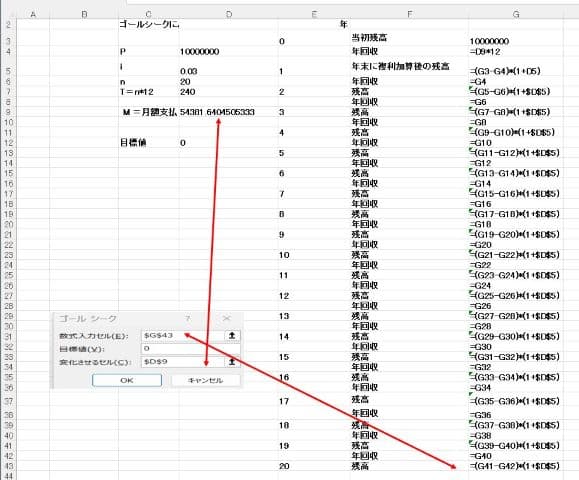
ゴールシークはエクセルの”データ”の”what-If"の中にある。ワークシートで計算モデルを作るときには変化させるセル(この事例では$D$9)に仮置きの数値、例えば1を入れておく。
このモデルを少し手直しすれば通常の月は毎月はX円引き出し、6月と12月は2X円引き出すような事例に応用できる。
このテキストファイルを開き全てを選択し(空白部分も含めて)コピーして、Excelの新しいシートの
セル番地A1にそのまま貼りつければ計算例のワークシートが再現できる。(Excel2016以降であれば可能、それより以前のversionではセルの分割作業が必要かもしれない)
Paste this text file directly into cell A1 of a new Excel sheet to recreate
the example worksheet
This is possible with Excel versions 2016 and later, but with earlier
versions you may need to split the cells
具体的な手順は以下のとおり
1 このテキストファイルを開く
2 すべてテキストを選択する
3 Excelの新しいシートに貼りつける
The specific steps are as follows:
1. Open this text file.
2. Select all the text.
3. Paste it into a new Excel sheet.
ただし資本回収係数の利用で注意しなければいけないことは、残高そのものが時価により変動しないことが前提となる。株式投信などで運悪く評価損が生じれば資金計画通りにはゆかなくなる恐れがある。評価損を避けたければ定期預金や国債等の満期保有で運用せざるを得ないが、その場合には1%の利回りどころか限りなくゼロ%に近い運用しかできない。そこで何らかの分散投資をするなどの工夫が必要になるが、これは誰も事前に最適解を求めることができない難しい問題である。結局、あれこれ考えて悩んでいても仕方ないので、たとえば上、中、下の3つシナリオを用意して、上のシナリオは週一回すき焼き、中のシナリオは月見うどん、下のシナリオは特売の湯豆腐としておき、流行り言葉で言えば、事態の推移を注視しつつ自らの支出(消費)行動をシナリオにあわせてスイッチしていくことになるだろう。予め資本回収係数を使って計算しておいた資金計画残高と比較しつつ、幸にも時価運用残高が増えているようであれば、すき焼きを食し、残念ながら時価運用残高が計画を下回っていれば特売の湯豆腐の生活に切り替えるような対応しか出来ないだろう。
少しまじめな話として、元本保証のないようなリスク資産の投資については事前に投資シミュレーションを行うことがよくある。モンテカルロ法によるシミュレーションはよく利用されるが、この場合にはシミュレーションに使われるモデルが妥当なものなのか注意しなければならない。モデルのパラメータを操作することで様々な将来図が描けてしまう。ファイナンス理論では株価のようなリスク資産価格の分析に幾何ブラウン運動に基づくモデルがよく使われる。例えば、初期価格35、ドリフト係数は0、株価のボラティリティが0.3と荒れ気味の設定でモンテカルロ・シミュレーションを行った一つの例では下図のように様々な株価の推移が描き出される。各時点での、その平均値を計算すると白色の線が示すように当初の価格35と変わらないといった結論を得る。
グラフ
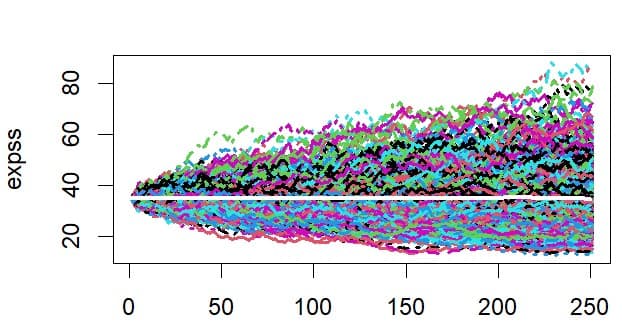
未来に、どの線が実現するのかは現時点では人間には分からないが様々な可能性があることは視覚的によく分かる。モデルの設定を操作すれば、いろいろな将来図を描けるがファイナンスの基礎理論から逸脱するようなモデルによるシミュレーションは自己責任で自分で楽しむ範囲内にとどめておくのが無難かもしれない。
余談として資本回収係数の導出の考え方について少しまとめてみる。
P=初期投資額 M=定額の引き出し額、i=利回り として、話を単純にするため3年間の運用と仮定する。
時点 投資残高
0 P
1 P(1+i)-M
2 (P(1+i)-M)(1+i)-M
3 ((P(1+i)-M)(1+i)-M)(1+i)-M
3年末での残高がゼロとなるようなMを求めることになる。
(1+i)=r と置き換えると
((Pr)-M)r-M)r-M=0 これを展開してゆくと
Pr³-Mr²-Mr-M =0 Mについて解くと
M=P×r³/(1+r+r²) ここで分母の(1+r+r²)は等比数列の和になるので等比数列の和の公式を使って(1-r³)/(1-r) で表せる。
従って、M/P=r³(1-r)/(1+r³) r=1+i を代入して整理すれば
M/P=-i・(1+i)³/(1-(1+i)³) =i・(1+i)³/((1+i)³-1)
任意の年数nについて求めるなら類推で上式の3をnに置き換えれば
資本回収係数 i・(1+i)ⁿ/((1+i)ⁿ-1) を得る。
基本的には、貨幣に時間価値がありキャッシュフローの発生時期で、その経済価値が異なるため、現在とか将来の時点間における価値変換(価値換算)をするという考え方によっている。