定率成長モデル（ゴードンモデル）

ゴードンモデルは内部留保のみで資金調達し、毎期に一定の利益の利益を生み、配当以外をすべて再投資して利益率（ＲＯＥ）ｒの収益を生み続けると仮定する。当期利益Ｅ、内部留保率ｂ（配当性向＝１－ｂ）、株主資本コストｋ、投資利益率（ＲＯＥ）ｒとすると株式価値V は

ｔ＝１の期の利益をＥとすれば配当金はＥ（１－ｂ）
ｔ＝２の期の利益はＥ＋Ｅｒｂ＝
Ｅ（１＋ｒｂ）
配当金は（１－ｂ）Ｅ（１＋ｒｂ）以下同様にしてｔ＝ｎの期では配当金は

これを配当割引モデルに代入すれば

という式１を得る。式１の両辺に（１＋ｋ）／（１＋ｂｒ）を乗じて式2

を導出し、式2から式1を差し引いて整理すると

を得る。

Vをｂで微分すると

ｒ＜ｋの場合はｄＶ／ｄｂ＜０，つまり内部留保率を高めると株価は減少していく。
ｒ＞ｋの場合はｄＶ／ｄｂ＞０、内部留保率を高めれば株価は上昇する。ｋ－ｒｂ＞０が前提条件なのでｂ＜ｋ／ｒ　の制約を受けるので内部留保率を１００％までは高めることは出来ずｋ／ｒが上限となる。ｋ＝ｒの時にはｄＶ／ｄｂ＝０で内部留保率は株価に影響を与えない。

ゴードンモデルは内部留保のみで資金調達し、毎期に一定の利益率(ROE)　ｒ　を生み、つまり再投資利益率がｒで一定という前提になっている。企業の追加投資が当期利益から行われると、この追加投資は利益率ｒで利益を生み出し利益増加をもたらす。つまり、

利益増加分＝追加投資×ｒ　　（式３）　
の関係となる。また、追加投資は当期利益のうち内部留保された部分から行われるので
追加投資＝当期利益×内部留保率　　（式４）　
の関係の成り立つ。（式４）を（式３）に代入すると
利益増加分＝当期利益×内部留保率×ｒ　　
となる。この式の両辺を当期利益で除すと
利益増加分／当期利益=
利益成長率ｇ＝内部留保率ｂ×ｒ　　の関係を得る。
従って g=b×r　となる。

例えば自己資本１００の企業が１０％利益率（ＲＯＥ）であれば当期利益は１００×０．１＝１０を生み出す。内部留保率が６０％であれば１０×０．６＝６が追加投資され自己資本は６だけ増加する。つまり成長率は６／１００＝６％になる。利益率ＲＯＥ×内部留保率は０．１×０．６＝６％　の関係が確認できる。
（補足説明）　通例によりROE＝当期利益／期首自己資本で計算すると仮定する。また配当支払いも当期利益から当期中に支払われると仮定する。現実には配当支払は決算確定の株主総会の後になるので期末資産は配当支払前の金額になるが、多くのテキストの計算例では期末時点で支払済と仮定している。従って、期首の資産が１００で、その資産を使って１０％の当期利益が稼得され、そのうちの４０％は配当流出で資産が１００×０．１×０．４＝４だけ減少する。つまり１００＋１０－４＝１０６が期末資産残高となる。これは期首資産残高１００よりも６％成長している。期首の資産は全て自己資本と仮定するので自己資本も１００×０．１×０．６＝６増加している。詳細はサスティナブル成長率をご参照）

もちろん実務的には再投資利益率がＲＯＥに等しく一定、あるいは内部留保率が一定といった条件を満たすことは希で常に可変的であり、株主資本コストと成長率の僅かの変動でも株式評価額に大きな差が生じやすいので株式評価の妥当性を多角的に検討する必要性はあるだろう。

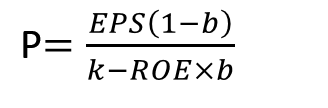このゴードンモデルに対してモジリアーニとミラーは配当政策は株価に影響しないと批判する。ゴードンモデルは内部留保だけで資金調達する前提に立っているので配当政策と投資政策は裏表の関係になって混同が生じていると批判する。アカデミックな世界での議論はいろいろと尽きない様子だが、実務的にはこのゴードンモデルはシンプルで変数も少なくて大変に扱いやすいメリットがある。次に、このゴードンモデルを使って株価収益率（ＰＥＲ）について若干の考察をしてみる。株価収益率（PER)は周知のように株価÷１株当り利益で計算される比率である。A社とB社の１株当り利益は同じなのにA社のPERは３倍でB社のPERは３０倍といったことはよく見られる。さらにはC社は赤字決算で１株当り利益はマイナスなのに市場では意外と高い価格で取引されていて、何かマーケットがおかしいのではないかと疑ったりすることはよく経験する。証券市場のアノマリーの１つとして低PER効果が有名であるが、これは低いPER銘柄は収益率が高い傾向が見られるという経験則である。この様なさまざまな現象を少し解き明かそうとする場合に配当割引モデルや定率成長モデルは大変に役に立つ。株価収益率の倍率の違いはどこから生じるのだろうか簡単な事例で検討してみたい。定率成長モデル（ゴードンモデル）は使い勝手がよいので、このモデルを使って以下のような条件を満たすA社について検討してみる。

ケース１　ROEが株主資本コストを上回る会社
A社
ＲＯＥ　　ｒ　　0.1
内部留保率　ｂ　　 0.6
成長率　ｇ＝ＲＯＥ×ｂ　 0.06
１株当たり利益　ＥＰＳ 10
資本コスト　ｋ　0.08

理論株価は
で計算できるので 10×(1-0.6)/(0.08-0.06)=200となる。200という株価はＡ社が６％の成長を無限に永続させたと仮定したものである。もしA社が利益全額を配当で支払い、成長を目指さないとすればｂ＝０となり、従ってｇ＝０なのでA社が全額配当ゼロ成長の場合の株価は 10×1/(0.08-0)=125となる。２００と１２５の差額の７５は成長機会の現在価値と考えることができる。ここから内部留保率を高め成長率を高めることが株価にプラスとなることがわかる。では、いつでも内部留保率を高めれば株価にプラスとなるのかケース２で確かめてみる。ケース２ではA社のROEと資本コストがそれぞれ０．１と同じ場合である。

ケース２　ROEが株主資本コストに等しい会社 ROE（ｒ）＝ｋの場合

Ｂ社
ＲＯＥ 0.1
内部留保率　ｂ 0.6
成長率　g＝ＲＯＥ×ｂ 0.06
１株当たり利益　
ＥＰＳ 10
資本コスト　ｋ　 0.1

式にあてはめると理論株価＝ 10×(1-0.6)/(0.1-0.06)=100 理論株価１００はＢ社のＲＯＥが株主資本コストと等しく１０％で無限に６％成長を続けたと仮定した場合の理論株価である。もしＢ社が利益全額を配当で支払い、成長を目指さないとすればｂ＝０となり、従ってｇ＝０なのでＢ社が全額配当でゼロ成長の場合の株価は（１０×１）/（０．１－０）＝１００となる。これは成長を織り込んだ株価と同一の１００となる。この原因はROEが０．１と資本コスト０．１と同じ率であることにより生じたものである。ここから、企業成長を目指すにはROEが資本コスト　ｋを上回っていること、つまり　ＲＯＥ　＞　ｋ　であることが必要なことがわかる。ROEが資本コストを上回らなければ内部留保率を高めても株価上昇には効果が無い。まずは資本コストを上回るROEが達成できるような経営をしなければならない。エクイティ・スプレッドが重要視される所以である。

上記の式の両辺をEPSで除すと下記のような株価収益率PERの算式が得られる。

PERが高くなるためには成長率が株主資本コストを上回らないという数学的な制約条件の下で高いROE、高い成長率あるいは低い資本コストが必要となる。高いPERの企業は高いROEや高い成長率の条件を満たしているためだろうと推測できる。アノマリーの一つである低PER効果については、一つの解釈としては新興企業は当初は利益も少なく変動幅も大きいため、投資家は高いリスクプレミアムを求めるので資本コストｋは大きくなり、成長率も低いので株価は低い傾向にあるが、少し軌道に乗り出すとＲＯＥは高くなり、キャッシュフローも安定して増加してくれば投資家の要求するリスクプレミアムも低くなり資本コストが下がってくると共に高い成長率が見込まれてくるので急激に株価が上がるケースも出てくるだろう。

ケース３　赤字会社、無配会社の評価新興企業Ｂ社はまだ創業して間もないので今後３年間は無配が予想されるが、４年目末には成長軌道に乗り始め、以下の条件で成長し続けると予想される。

ＲＯＥ（ｒ） 0.1
内部留保率　ｂ 0.6
成長率　g＝ＲＯＥ×ｂ 0.06
１株当たり利益　
ＥＰＳ 10
資本コスト　ｋ 0.08

3年間は赤字のため配当は期待できないが、今から４年後の時点でのゴードンモデルによる予想株価は下記の計算のように２００（4年後の予想株価）となる。

10*(1-0.6)/(0.08-0.06)=200

この会社の現時点での理論株価は１４７

となるので、仮に現在の株価が１３０であれば、赤字企業であったとしても割安と判断される。一般にアナリストが株価評価モデルを使って理論株価を計算するときには決算短信などのデータを単純に引用することはなく、様々なシナリオ分析などを併用し企業の経済的利益（economic earnings,economic incomes)を追求していると考えられる。経済的利益はなんぞやと言い出すと大変に奥が深く、遂にはヒックス（Hiｃks)とかハイエク(Hayek)といった歴史上の大経済学者が登場してきてしまい、全く手に負えなくなるが、大ざっぱに言えば企業が永続的に事業活動をして成長を維持するためのネット・キャッシュフローで、時価評価した純資産の変化額といえる。アナリストは様々な仮定を置いたりして、企業の財務数値を経済的利益の代理変数として使っているものと思われる。例えば、通常は研究開発費や広告宣伝費は会計上は期間費用として処理されているが、これらの支出は将来的に企業にキャッシュフローをもたらす可能性があり無形資産に対する投資として見ることも可能なので、企業評価にも大きな影響を及ぼし得る。将来のキャッシュフローの可能性の見方なので、他の無形知的資産の評価と同様にどのように価値評価するかは難しい問題の一つとされている。実務上は資本コストをどのように算定するも問題の一つになるが、資本資産評価モデル（CAPM)を応用する方法も広く使われている。

投資家の視点から見たゴードンモデルについて

これでは主として株価評価の観点でゴードン・モデルを検討してきたが、ここからは市場が企業の成長力をどの様に評価しているかを探るツールとして検討してみる。

の算式では分子は1株当たり配当、分母は（資本コスト－成長率）と読むことが出来る。資本コストの実証研究は多数発表されているが、日本企業では5％から8％くらいの推定をよく目にする。上記算式のうち配当は公開されており、資本コストの業種別の平均値なども入手しやすいかも知れない。もし入手できなければ仮に5％などと仮定できる。企業の株価は終値などで把握できる。するとモデルの他の変数を所与として、終値から成長率を逆算することが出来る。マーケットでは当該企業の成長率をどの様に見ているかを探るヒントになるかも知れない。オプション価格からインプライド・ボラティリティを推計するのと同様の手法である。例えば終値が100、配当は5、資本コスト8％とすれば100=5/(0.08-x) でｘ＝0.03から成長率を3％と見ていると推測できる。これでは余りに素朴すぎると思えば、少し手間をかけて、三角分布など適当な変数の確率分布を想定してモンテカルロ・シミュレーションを行うことにより成長率の確率分布を探ることも可能だろう。

サスティナブル成長率

ROEの３指標分解（デュポンシステム）

財務入門目次へ