1. ホーム
  2. 金融工学を初等数学で
  3. ブラック・ショールズ　モデルとデルタ

MAXIMAによるブラック・ショールズ　モデル

ブラック・ショールズモデルとデルタ ブラック・ショールズモデルはファイナンスの理論では古典的でしかも重要なテーマになっており、専門書も多数出版されている。レベルも様々で書籍によって読者に要求する数学のレベルにも幅があるが、入門書と表題がついていても数式の羅列ばかりで私のような文系の人には取っつきにくいものが多い。しかし幸いなことに数学ソフトを使ってモデルにいろいろな数値を当てはめて計算させたりグラフ表示をさせて遊んでいると感覚的に理解が少し進むように思える。ここではMAXIMAを使ってオプション・プライシングとデルタの導出、計算を試みる。教科書としては私の場合は、邦書では　よくわかるブラック・ショールズ・モデル　蓑谷千凰彦　東洋経済新報社　２０００年3月発行　　洋書としては Fundamentals of futures and options markets  John c. Hull 5th Prentice Hall  を気に入っている。「よくわかるブラック・ショールズモデル」は数式の展開、説明が丁寧で文系の人にわかりやすいと思う。　John Hull の書籍は上級者向けのOptions,Futures and other derivatives もあるがHullの書籍は何れもstudy guide ないし　solutions manual が書店で購入できるので独学自習する場合には大変に便利である。そこでHullのFundamentals of futures．．．　の例題を参考にしてmaximaを使ってブラックショルズ式の意味などの入門的自習を試みた。　まず標準正規分布の累積密度関数をつかうのでmaximaのdistrib というパッケージを読み込む。ｓ＝原資産価格（ここでは株式時価　ｘ＝権利行使価格、ｒ＝利子率、Ｔ＝満期までの期間（年率換算するので、例えば満期まで１５日の場合は１５／３６５　σ＝ボラティリティ、、ｄ１、ｄ２　はそれぞれの定義式に従いコールオプションの価格式を定義すると以下のようになる。\( \DeclareMathOperator{\abs}{abs} \newcommand{\ensuremath}[1]{\mbox{$#1$}} \)
(%i1) load(distrib)$
(%i2) snormal(y):=cdf_normal(y,0,1);
\[\tag{%o2} \operatorname{snormal}(y):=\operatorname{cdf\_ normal}\left( y,0,1\right) \]
--> /* 正規密度関数を定義 */;
--> /*  正規累積密度関数を定義 */;
--> /* 以下はブラックショールズのコールオプション式を定義 */;
--> /* s=株式時価　ｘ＝権利行使価格　sigma＝年率ボラティリティ（標準偏差） */;
--> /* Ｔ＝残存年数（残存日数３０日なら　Ｔ＝３０／３６５　ｒ＝年率金利　*/;
(%i3) d1(s, x, sigma, T, r):=(log(s/x)+(r+sigma^2/2)*T)/(sigma*sqrt(T));
\[\tag{%o3} \operatorname{d1}\left( s,x,sigma,T,r\right) :=\frac{\log{\left( \frac{s}{x}\right) }+\left( r+\frac{{{sigma}^{2}}}{2}\right) T}{sigma \sqrt{T}}\]
(%i4) d2(s, x, sigma, T, r):=d1(s, x, sigma, T, r)-sigma*sqrt(T);
\[\tag{%o4} \operatorname{d2}\left( s,x,sigma,T,r\right) :=\operatorname{d1}\left( s,x,sigma,T,r\right) -sigma \sqrt{T}\]
上記のコール価格式にＨｕｌｌ　の例題に従って、株価　s=42,　権利行使価格　x=40, ボラティリティ　σ=0.2 満期までの期間　T=0.5, 利子率　r =0.1 を代入するとコールオプションの価格が求まる。プットオプションもプットコールパリティを使ってプット価格も計算できる。
(%i6) float(bsCall(42, 40, 0.2, 0.5, 0.1));
\[\tag{%o6} 4.759422392871535\]
(%i7) dd1:float(d1(42, 40, 0.2, 0.5, 0.1));
\[\tag{dd1}0.7692626281060315\]
(%i8) bsPut(s,x,sigma,T,r):=bsCall(s,x,sigma,T,r)+x*exp(-r*T)-s$
(%i9) float(bsPut(42, 40, 0.2, 0.5, 0.1));
\[\tag{%o9} 0.8085993729000975\]

コール価格が株式時価の動きに従って、どのように変化するかをグラフで見ると以下のようになる。
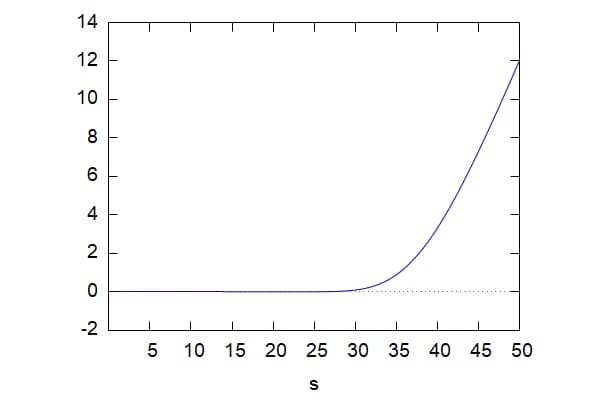
(%i10) wxplot2d(bsCall(s, 40, 0.2,0.5, 0.1),[s,0.01,50]);
\[\tag{%t10} \] ブラックショールズモデル　コール価格
\[\tag{%o10} \]
プット価格の動きは以下のようになる。
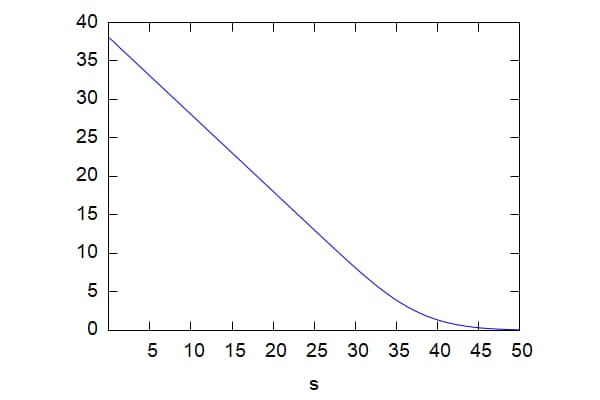
(%i11) wxplot2d(bsPut(s, 40, 0.2,0.5, 0.1),[s,0.01,50]);
\[\tag{%t11} \] ブラックショールズモデル　プット価格
\[\tag{%o11} \]
  /*  累積密度関数を微分すれば密度関数となる  */;   
オプションのデルタについてオプションのデルタはコールの価格式を株価ｓで偏微分すれば求まるが、これが意外に一筋縄ではいかない。何故なら正規分布関数の引数ｄ１、　ｄ２　にはｓが含まれており、ややこしい合成関数の微分となってしまう。この辺の証明は上記のよくわかるブラック・ショールズモデル　蓑谷千凰彦　に書かれているので、それを参考にして数式処理する。なお、HullのOptions,Futures and other derivatives では練習問題として取り上げられており、Solutions manualの中で詳しい証明が示されている。 

\[\frac{\partial C}{\partial s}= Φ(d1)+\{s・ \frac{\partial Φ(d1)}{\partial s}-x・ exp^{-rT} \frac{\partial Φ(d2)}{\partial s}\}  \]



上式は株価ｓで偏微分した結果になるが｛　｝で括った部分がゼロとなることが確かめられればデルタはΦ（d1)　つまり標準正規分布関数となる。括弧の部分がゼロとなることをmaximaで確かめると以下のようになる。
(%i12) z1:diff(snormal(d1),d1);
\[\tag{z1}\frac{{{\% e}^{-\frac{{{\mathit{d1}}^{2}}}{2}}}}{\sqrt{2}\, \sqrt{\ensuremath{\pi} }}\]
(%i13) z2:diff(d1(s, x, sigma, T, r),s);
\[\tag{z2}\frac{1}{\sqrt{T} s sigma}\]
(%i14) z3:z1*z2;
\[\tag{z3}\frac{{{\% e}^{-\frac{{{\mathit{d1}}^{2}}}{2}}}}{\sqrt{2}\, \sqrt{\ensuremath{\pi} }\, \sqrt{T} s sigma}\]
(%i15) z4:diff(snormal(d2),d2);
\[\tag{z4}\frac{{{\% e}^{-\frac{{{\mathit{d2}}^{2}}}{2}}}}{\sqrt{2}\, \sqrt{\ensuremath{\pi} }}\]
(%i16) z5:s*z1-x*exp(-r*T)*z4;
\[\tag{z5}\frac{{{\% e}^{-\frac{{{\mathit{d1}}^{2}}}{2}}} s}{\sqrt{2}\, \sqrt{\ensuremath{\pi} }}-\frac{{{\% e}^{-T r-\frac{{{\mathit{d2}}^{2}}}{2}}} x}{\sqrt{2}\, \sqrt{\ensuremath{\pi} }}\]
--> /* subst(代入する式,変数名,式)は(式ｚ5式)中の(変数-d1^2/2)に   */;
--> /* (代入する式(-r*T-log(s/x)-d2^2/2))を代入する  */;
(%i17) z6:subst((-r*T-log(s/x)-d2^2/2),-d1^2/2,z5);
\[\tag{z6}0\]
括弧の中がゼロとなることが分かる。
（デルタ導出の数式処理については　ブラック・ショールズ・モデルのデルタ導出過程とリスク中立世界でのN(d1)、N(d2)の考え方　参照）
(%i18) DELT:z1+z6;
\[\tag{DELT}\frac{{{\% e}^{-\frac{{{\mathit{d1}}^{2}}}{2}}}}{\sqrt{2}\, \sqrt{\ensuremath{\pi} }}\] 株価　s=42,　権利行使価格　x=40, ボラティリティ　σ=0.2 満期までの期間　T=0.5, 利子率　r =0.1 をデルタの式に代入するとデルタが求まる
(%i19) define (Delta(s, x, sigma, T, r),diff(bsCall(s, x, sigma, T, r),s))$
(%i20) float(Delta(42, 40, 0.2, 0.5, 0.1));
\[\tag{%o20} 0.7791312909426681\]
このデルタはデルタヘッジの必要枚数の計算に使われる。株価５０までのデルタの変化をグラフにする。デルタは原資産価格（株価）とともに変化することが分かる。デルタヘッジをする場合には株価の変化に対応してヘッジのリバランスをしなければならない。
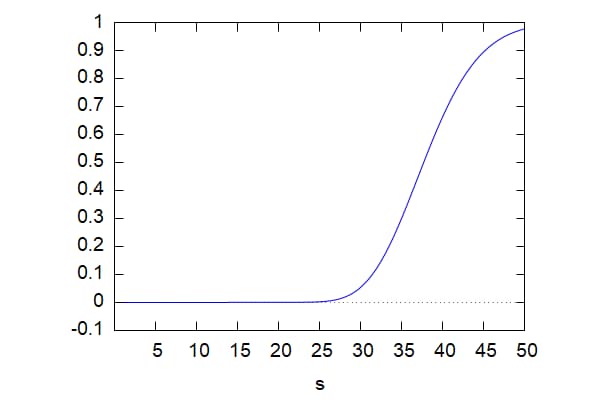
(%i21) wxplot2d(Delta(s, 40, 0.2,0.5, 0.1),[s,0.01,50]);
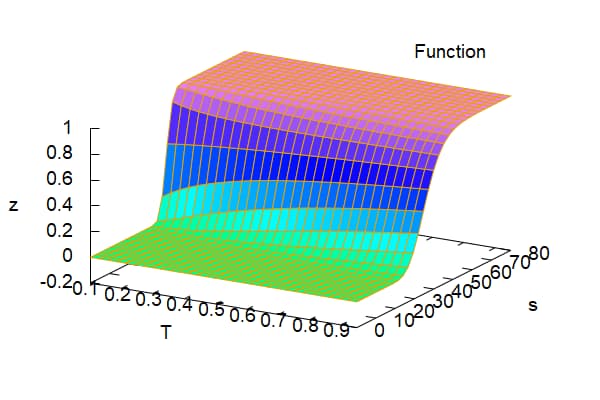
\[\tag{%t21} \] ブラックショールズモデル　デルタ
\[\tag{%o21} \]
残存時間を０から０．９５まで、株価を０．１から８０まで変化させると以下のようになる。
(%i22) wxplot3d(Delta(s, 40, 0.2,T, 0.1),[T,0.1,0.95],[s,0.1,80]);
\[\tag{%t22} \] ブラックショールズモデル　デルタ
\[\tag{%o22} \]




MAXIMAによるオプション・グリークス





金融工学を初等数学で　目次