-
ホーム
-
金融工学を初等数学で
-
オプショングリークス
オプショングリークス(セータ、ガンマ、ベガ)とインプライド・ボラティリティ,ベガ・コンベキシティ,ボルガ(VEGA CONVEXITY,VOLGA)の計算
ブラック・ショールズモデルについて、価格式を原資産価格s、ボラティリティσ、残存期間T、利子率rなどで偏微分すると各変数が1単位変化した場合のオプション価格変化を測定できる。これらの指標はギリシャ文字を使って表す慣例になっていて、トレーダーのリスク管理指標やシナリオ分析に使われている。
前に、MAXIMAを使ってオプション・プライシングとデルタの導出、計算を試みたが、次に、セータ、ガンマ、ベガなど他のオプショングリークスの計算を試みる。
ここでの計算例はデルタの導出、計算例と同様に s=42, 権利行使価格 x=40, ボラティリティ σ=0.2 満期までの期間 T=0.5, 利子率 r =0.1
ヨーロッパ型コールオプションとして、MAXIMAを使って計算する。
\( \DeclareMathOperator{\abs}{abs}
\newcommand{\ensuremath}[1]{\mbox{$#1$}}
\)
\[\tag{%o0} \mathit{done}\]
|
-->
|
snormal(y):=cdf_normal(y,0,1); |
\[\tag{%o2} \operatorname{snormal}(y):=\operatorname{cdf\_ normal}\left( y,0,1\right) \]
|
-->
|
/* 以下はブラックショールズのコールオプション式を定義 */; |
|
-->
|
/* s=株式時価 x=権利行使価格 sigma=年率ボラティリティ(標準偏差) */; |
|
-->
|
/* T=残存年数(残存日数30日なら T=30/365 r=年率金利 */; |
|
-->
|
d1(s, x, sigma, T, r):=(log(s/x)+(r+sigma^2/2)*T)/(sigma*sqrt(T)); |
\[\tag{%o3} \operatorname{d1}\left( s,x,sigma,T,r\right) :=\frac{\log{\left( \frac{s}{x}\right) }+\left( r+\frac{{{sigma}^{2}}}{2}\right) T}{sigma \sqrt{T}}\]
|
-->
|
d2(s, x, sigma, T, r):=d1(s, x, sigma, T, r)-sigma*sqrt(T); |
\[\tag{%o4} \operatorname{d2}\left( s,x,sigma,T,r\right) :=\operatorname{d1}\left( s,x,sigma,T,r\right) -sigma \sqrt{T}\]
|
-->
|
bsCall(s, x, sigma, T, r):=s*snormal(d1(s,x,sigma,T,r))-x*
exp(-r*T)*snormal(d2(s,x,sigma,T,r))$ |
|
-->
|
define (Delta(s, x, sigma, T, r),diff(bsCall(s, x, sigma, T, r),s))$ |
|
-->
|
Delta(42, 40, 0.2, 0.5, 0.1)$ |
\[\tag{%o8} 0.7791312909426681\]
|
-->
|
wxplot2d(Delta(s, 40, 0.2,0.5, 0.1),[s,0.01,50]); |
\[\tag{%t9} \]
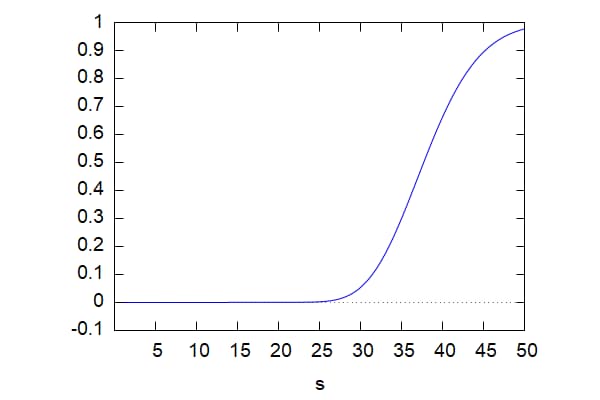
\[\tag{%o9} \]
|
-->
|
wxplot3d(Delta(s, 40, 0.2,T, 0.1),[T,0.1,0.95],[s,0.1,80]); |
\[\tag{%t10} \]
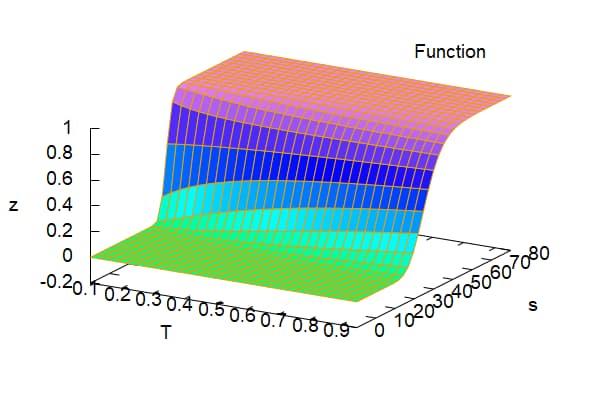
\[\tag{%o10} \]
デルタ以外のグリークス(セータ、ガンマ、ベガ)指標についてMAXIMAで記述すると以下のようになる。ここではTは満期までの残存時間として定義している。満期日は何月何日という確定数値なので、これをTT、経過してゆく変数としての時間をtとすると時間の経過とともにtはTTという満期日(確定数値)に収束していく。つまりT=TT-t
という関係が成り立っており、満期日にはゼロとなる。オプション価格は時間変数tについてみれば減少関数となっており、時間が経過するとともに、つまりtがTTに近くにつれて価値が減少していく。セータ(Theta)を求めるにはコール価格を時間変数tで偏微分するが
\[T = TT-t\] \[\frac{\partial T}{\partial
t}=0-1\]\[\frac{\partial{C}}{\partial{t}}=\frac{\partial{C}}{\partial{T}}
\frac{\partial{T}}{\partial{t}} =(-1)\frac{\partial{C}}{\partial{T}} \]という関係を使って以下の式で示せる。時間経過とともにオプション価値が低下するというタイムディケイ(TIME
DECAY)を表している。
|
-->
|
define (Theta(s, x, sigma, T, r),-diff(bsCall(s, x, sigma, T, r),T))$ |
|
-->
|
float(Theta(42, 40, 0.2, 0.5, 0.1)); |
\[\tag{%o13} -4.55909219459263\]
|
-->
|
/* 1日当りのセータ Theta/365 */; |
\[\tag{%o14} -0.01249066354682912\]
|
-->
|
wxplot2d(Theta(s, 40, 0.2,0.5, 0.1),[s,0.01,50]); |
\[\tag{%t15} \]
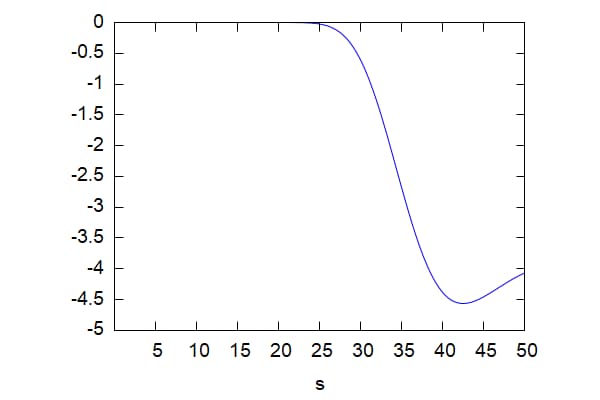
\[\tag{%o15} \]
計算式の意味を考えると、セータの値は-4.559... この値は1年間の数値なので、一日当たりのセータは-0.01249 。オプションの時間価値が他の条件が一定であれば1日経過するごとに0.01249減価することを示している。原資産価格の変化とともにセータは図のように変化していく。ATMでセータの絶対値は最大となっている|
-->
|
float(Gamma(42, 40, 0.2, 0.5, 0.1)); |
\[\tag{%o17} 0.04996267040591196\]
|
-->
|
wxplot2d(Gamma(s, 40, 0.2,0.5, 0.1),[s,0.01,50]); |
\[\tag{%t18} \]
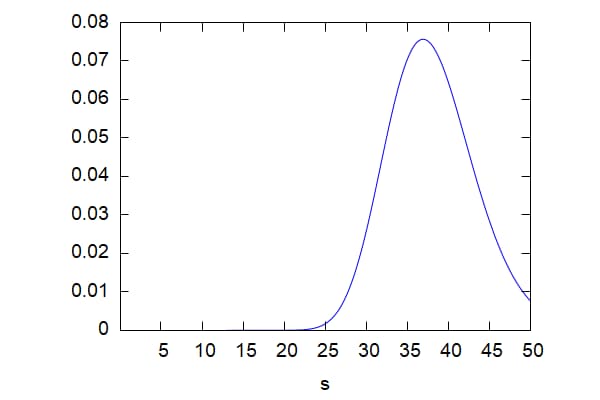
\[\tag{%o18} \]
ガンマは原資産価格に対するデルタの変化率を表しており、オプションの価格曲線の曲率で、その値は約0.05、原資産価格の変化とともにガンマは図のように変化していく。ATMで最大となっている。ガンマが大きいことはデルタの原資産価格に対する感応度が高いことを意味しヘッジ比率の頻繁な見直しが必要となる。
ベガはボラティリティに対するオプション価格の変化率を示しておりATMで最大となっている。ブラックショールズ式はもともとボラティ
リティは一定との前提で導出された式であるが、現実にはボラティリ
ティは時間とともに変化する点に注意すべきである。この辺りの詳しい議論
は専門書を参照されたい。デルタヘッジをして原資産価格の変動リスクを削減したと思っても、ボラティリティの変動リスクはなお残されている。
|
-->
|
define (Vega(s, x, sigma, T, r),diff(bsCall(s, x, sigma, T, r),sigma))$ |
|
-->
|
float(Vega(42, 40, 0.2, 0.5, 0.1)); |
\[\tag{%o20} 8.813415059602882\]
|
-->
|
/* 1%当たりのボラティリティは、Vega×0.01 */
; |
\[\tag{%o21} 0.08813415059602882\]
|
-->
|
wxplot2d(Vega(s, 40, 0.2,0.5, 0.1),[s,0.01,50]); |
\[\tag{%t22} \]
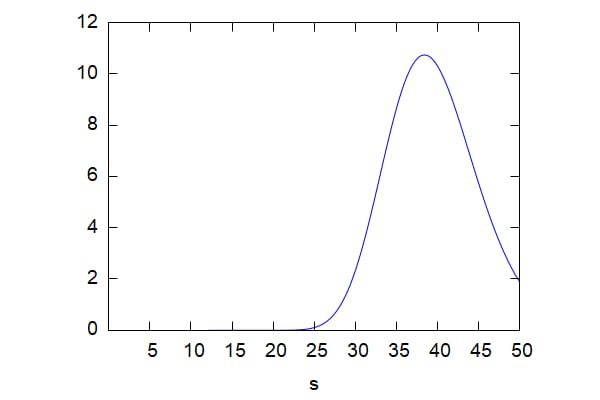
\[\tag{%o22} \]
株価を0.1から50まで、残存年数を0.1から0.95まで変化させた場合のベガを3次元グラフで示すと以下のようになる。
|
-->
|
wxplot3d(Vega(s, 40, 0.2,T, 0.1),[T,0.1,0.95],[s,0.1,50]); |
\[\tag{%t23} \]
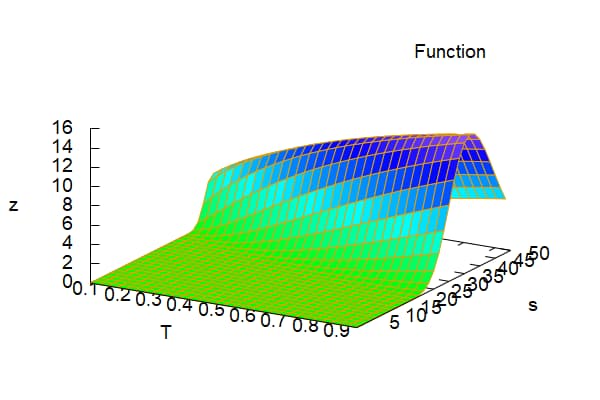
\[\tag{%o23} \]
次にインプライド・ボラティリティ(implied volatility)の計算をMAXIMAで試みる。
Hull のテキストでインプライド・ボラティリティの計算例が示されているが、ヨーロッパ型のコールオプションで オプション価格は1.9 株価
s=21、権利行使価格 x=20、利子率r=0.1 残存期間T =0.25 の条件下でインプライド・ボラティリティをMAXIMAで計算すると以下のようになる。ブラック・ショールズ・モデルのうち、ボラティリティを未知数として、オプション理論価格が所与の原資産価格(株価)、金利、残存時間、権利行使価格を前提とした場合に市場で成立しているオプション価格に等しくなるようなボラティリティを計算する。これは代数的には解けないので数値解析でオプション・モデルによる理論価格=オプション市場価格 となるようなボラティリティ(ここではsigma)を求めている。
|
-->
|
/* implied volatility の計算 find_root で現在のコール価格に等しくなるsigmaを */; |
|
-->
|
Impvola(s,x,T,r,cprice):=find_root(bsCall(s,x,sigma,T,r)-cprice,sigma,0.05,0.9)$ |
|
-->
|
float(Impvola(17000,17500,30/365,0.004,1000)); |
\[\tag{%o25} 0.6251129402236006\]
ブラック・ショールズのオプション価格式のうちボラティリティは観測できない数値のため、過去の株価のボラティリティから推測したりする。しかし推定期間によってボラティリティの推定値は変化するので、予測が難しい。そこで発想を変えて,マーケットではすべての情報を織り込んで価格が成立していると仮定すれば現在のオプション価格から権利行使価格、利子率、残存期間は既知として価格式からボラティリティを逆算したのがインプライドボラティリティ(implied
volatility)である。アットザマネー(ATM)のオプションのインプライドボラティリティは信頼性が高いと言われている。
インプライド・ボラティリティの計算では、ブラック・ショールズ・モデルのうち、ボラティリティを未知数として、オプション理論価格が所与の原資産価格(株価)、金利、残存時間、権利行使価格を前提とした場合に市場で成立しているオプション価格に等しくなるようなボラティリティを計算している。この考え方を応用すると、原資産価格(株価)を未知数として、所与のオプション価格、ボラティリティ、金利、残存時間、権利行使価格を前提とした場合の株価
implied
priceが計算できる。ブラックショールズモデルに基づいて、現在のオプション価格から見た理論株価を逆算しようとする試みである。単なる数値計算の遊びかもしれないが、市場の過剰反応の度合いを探る何らかのヒントになるかもしれないと思い、MAXIMAで試算してみた。
|
-->
|
/* コール価格から株価を数値解析で逆算する */; |
|
-->
|
Impstk(x,sigma,T,r,cprice):=find_root(bsCall(s,x,sigma,T,r)-cprice,s,1000,50000)$ |
|
-->
|
float(Impstk(17500,0.253,30/365,0.004,600)); |
\[\tag{%o27} 17667.62789089889\]
|
上記のコール価格式に、株価 s=42, 権利行使価格 x=40, ボラティリティ σ=0.2
満期までの期間 T=0.5, 利子率 r =0.1
を代入するとコールオプションの価格が求まるが、この計算だけではつまらないので、ちょっと横路に入るが、株価sと権利行使価格xを各10倍、1000倍とした時のコール価格を求めてみた。するとコール価格もちょうど10倍、1000倍となって返ってきた。この事から推論するとブラックショールズモデルは株価、権利行使価格について一次同次式になっているように思える。 |
\[\tag{%o28} 4.759422392871535\]
|
-->
|
float(bsCall(420, 400, 0.2, 0.5, 0.1)); |
\[\tag{%o29} 47.59422392871534\]
|
-->
|
float(bsCall(42000, 40000, 0.2, 0.5, 0.1)); |
\[\tag{%o30} 4759.422392871533\]
横道にそれたが、本題のインプライドボラティリティを計算してみる。株価s=23300、権利行使価格x=24000 残存時間T=15日 つまり15/365 コール価格cprice=71とするとインプライドボラティリティは下記のように15.7%と計算できる
|
-->
|
/* implied volatility の計算 find_root で現在のコール価格に等しくなるsigmaを */; |
|
-->
|
Impvola(s,x,T,r,cprice):=find_root(bsCall(s,x,sigma,T,r)-cprice,sigma,0.01,0.99)$ |
|
-->
|
float(Impvola(23300,24000,15/365,0,71)); |
\[\tag{%o32} 0.1565879664257076\]
上記と同一の条件下でコール価格が50から100まで変化した場合のインプライドボラティリティは下記のようにコール価格上昇とともに、高まっていく。|
-->
|
wxplot2d(Impvola(23300, 24000,15/365,0,cprice),[cprice,50,100]);; |
\[\tag{%t33} \]
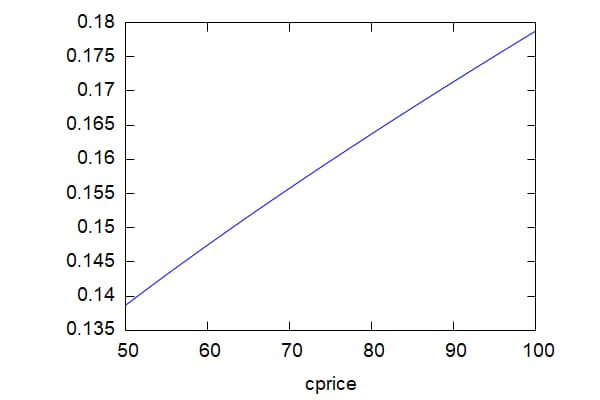
\[\tag{%o33} \]
上記の
インプライドボラティリティの計算法を応用して、原資産価格(株価)を未知数として、所与のオプション価格、ボラティリティ、金利、残存時間、権利行使価格を前提とした場合の株価
implied
priceを計算してみる。条件は権利行使価格x=24000 ボラティリティσ=0.16 残存日数15日 つまりT=15/365,オプション価格cprice=75、|
-->
|
Impstk(x,sigma,T,r,cprice):=find_root(bsCall(s,x,sigma,T,r)-cprice,s,10,500000)$ |
|
-->
|
float(Impstk(24000,0.16,15/365,0,75)); |
\[\tag{%o35} 23298.57384032603\]
上記の条件下でのインプライドプライスは約23300と計算されている。前提条件を権利行使価格x=24000 ボラティリティσ=0.2 残存日数15日 つまりT=15/365,金利ゼロ としてオプション価格を50から100まで変化させたときのグラフを描くと下記のようになる。
|
-->
|
float(Impstk(24000,0.2,15/365,0,80)); |
\[\tag{%o36} 23049.85129101646\]
|
-->
|
wxplot2d(Impstk(24000,0.2,15/365,0,cprice),[cprice,50,100]); |
\[\tag{%t37} \]
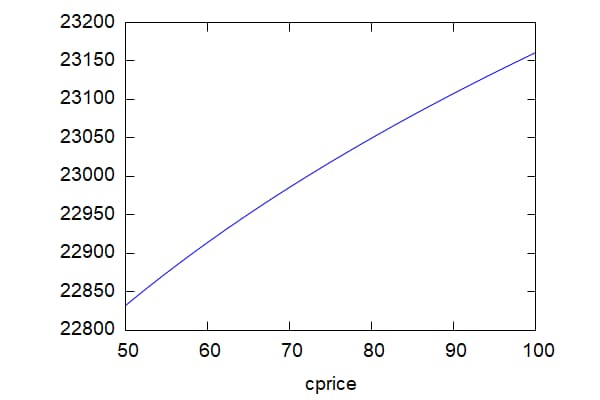
\[\tag{%o37} \]
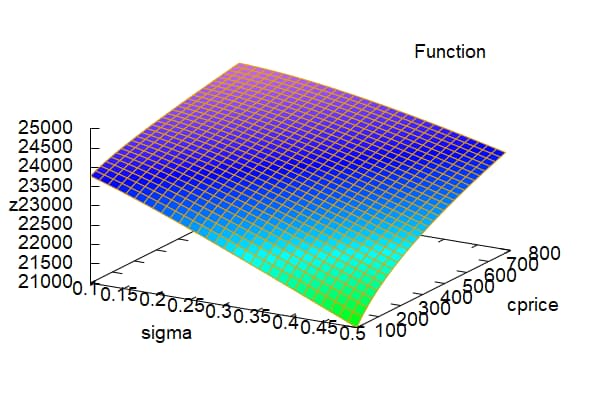
オプション価格を100から800まで、ボラティリティを0.1から0.5まで変化させたときのグラフを描くと下記のようになる。|
-->
|
wxplot3d(Impstk(24000,sigma,15/365,0,cprice),[sigma,0.1,0.5],[cprice,100,800]); |
\[\tag{%t38} \]
\[\tag{%o38} \]
先ほど、ブラックショールズ式についてボラティリティ(sigma)で偏微分してベガを計算したが、このベガについてはボラティリティ(sigma)で偏微分(つまりブラックショールズ式について2次微分)したものをVEGA
CONVEXITYあるいはVOLGA,あるいはVOMMAと呼んでいる。
\[\frac{\partial^2 C}{\partial σ^2}=Vega\frac{d1 d2} {σ} \]
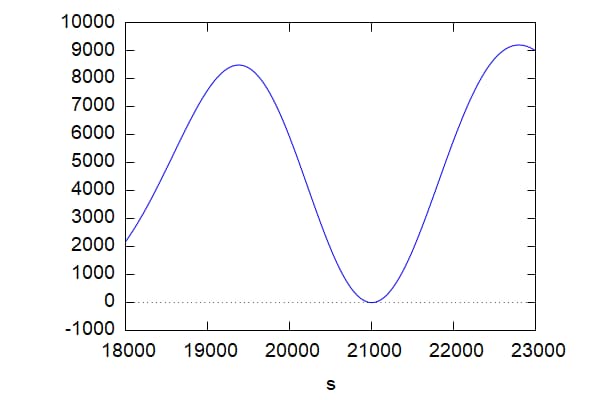
これはボラティリティの変化に対するベガ(VEGA)の変化率を示している。慣例として10000で除して利用されている。VOLGAはATMで最小となっており、アウトオブザマネー(OTM)最大となっていることが見て取れる。OTMのオプションのベガはボラティリティの変化に対して感応度が高くなっている。
| (%i38) |
define (ConvexVega(s,x,sigma,
T, r),diff(Vega(s,
x, sigma,
T, r),sigma))$ |
株式時価 20000 権利行使価格 21000 ボラティリティ20% 満期までの日数30日 金利ゼロ とした場合のベガ コンベキシティは以下のように計算できる。
| (%i39) |
float(ConvexVega(20000,21000,0.2,30/365,0)); |
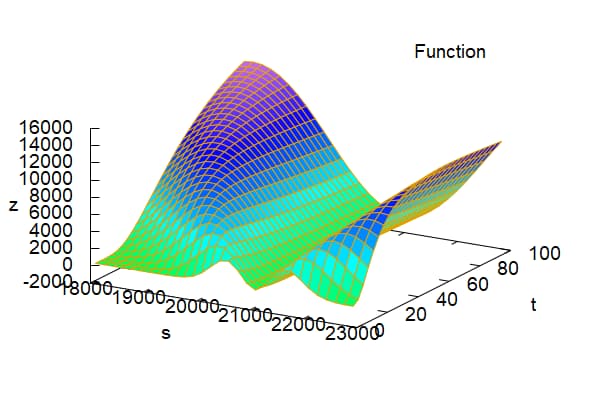
株式時価を18000から23000まで、残存日数を0から100日まで変化させた場合のvega
convexity(volga,vomma)をグラフ化すると以下のようになる。
| (%i59) |
wxplot3d(ConvexVega(s,21000,0.2,t/365,0.00),[s,18000,23000],[t,0,100]); |
| (%i60) |
wxplot2d(ConvexVega(s,21000,0.2,30/365,0.00),[s,18000,23000]); |
\[\tag{%o60} \]
金融工学を初等数学で 目次










