準分散、ソルティノレシオ、LPM、UPMの計算例 in Excel
numerical examples of semivariance,Sortino ratio,LPM,UPM in Excel
マーコヴィツ流のポートフォリオ分析では収益率の平均と分散に着目した投資管理が行われる。例えば目標収益率を達成するするのに最小の分散となるポートフォリオが選択されるか、あるいは一定の分散の範囲内で最大の収益率を達成できるポートフォリオが選択される。ここで分散(あるいはその平方根である標準偏差)はリスク尺度として重要な役割を果たしている。
しかしマーコヴィツも当時から指摘していたように収益率の分布が正規分布のように左右対称型であれば通常の分散をリスク尺度とすることは支障ないが、もし収益率の分布が正規分布でなく歪んでいる場合には下方リスクに着目した準分散を使ってリスク指標とすべきと提唱していた。この場合、ポートフォリオの分散共分散行列が対称行列にならず計算が複雑で、1950年代のコンピュータの性能では時間とコストがかかるといった理由などでこのアイディアは普及しなかった。しかし研究者の中では準分散などの考え方を発展させLPM(Lower
Partial Moment),UPM(Upper Partial
Moment)などを指標とするポートフォリオ選択やそのアルゴリズムが研究されてきた。この間にコンピュータの性能も大きく向上したことも支えとなっているようだ。
準分散の計算
通常の分散は平均値を中心としてその上下のバラツキの程度を測定するが、準分散は平均値の下側のバラツキに着目し、平均値以上のバラツキはゼロとして計算される。さらには平均値にこだわらず適当な目標値を指定し、その目標値以下のバラツキを測定することもできる。汎用的な式で示すと下記のように表せる。ここで目標収益率に平均値を指定することも出来る。
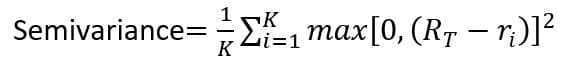
K 標本数、RT 目標収益率 ri 毎期の収益率
この算式の中でmaxは目標収益率を例えば0.1とすれば利益率0.15のデータは目標値より大きいので0.1-0.15=-0.05となる。この-0.05とゼロを比べればゼロの方が大きいので2者のうちより大きいゼロの方を返してくる。
RT 目標収益率には必要に応じて平均収益率、安全資産利子率、インフレ率、適当なベンチマーク収益率などが用いられる。
ソルティノレシオの計算
ソルティノレシオの計算では分母に準分散の平方根が用いられる。
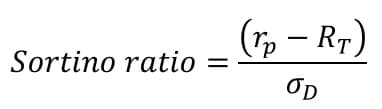
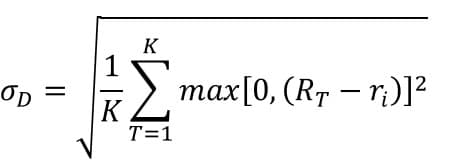
σD
はポートフォリオの準分散の平方根、rpはポートフォリオの収益率、RTはターゲット収益率で平均収益率その他が用いられる。下方リスクに対するターゲットからの超過収益率の比率となっており、この比率が高いほど下方リスクに対する強さを表していると解釈できる。
簡単な計算例
過去4年間のポートフォリオの収益率が
(0.2, -0.15, -0.1, 0.3)だったとする。
標本数K=4,平均収益率は4年間の算術平均を求めれば0.0625となる。ターゲット収益率を0.05としてソルティノレシオをエクセルで計算すると下表のようになる。

念のため数式表示では

上の計算からも明らかなように
min(0,r-RT)とmax(0,RT-r)は同じ計算をしている。どちらの式を使っても同一の結果を得る。
ターゲット収益率を5%に設定した場合ソルティノレシオはポートフォリオの平均収益率が6.25%なので(0.0625-0.05)/0.125=0.1 となる。
シャープレシオも超過収益率を標準偏差で除して求めるが、シャープレシオで使われる標準偏差は通常の分散、つまり平均値を中心として下方、上方の両方向に対する収益率のバラツキであり、上方向への上振れもリスクとして扱われている。通常の投資家は買い持ち、つまりロングポジションとすれば収益率が平均より上回ることは良い、好ましいリスクであるが下振れリスクと同様にひとつのリスクとして扱われている。しかし、ソルティノレシオは準分散を応用し下方、つまり収益率の分布では左側(negative
skewness)ともいわれるブレ(つまり左側のテールリスク)に対のする強さの程度を示している。ポートフォリオの中で相場の下落局面での相対的な強さを比較するのに便利な指標といえる。
LPM,UPM
準分散は偏差の2乗で投資家のリスク回避度を測定したが、これを統計学の積率の考え方を応用しリスク愛好的、中立的、回避的の度合いを測定できるような指標が考案された。それがLPM(Lower
Partial Moment)である。
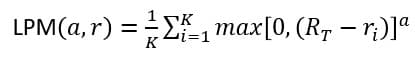
K 標本数、RT 目標収益率 ri 毎期の収益率
a 次数
準分散の式ではa=2であったが、LPMでは1,2,3といった正の整数だけでなく3.14といった実数も使えるようになっている。
0<a<1であれば投資家はリスク愛好的
a>1 であればリスク回避的
a=1 であればリスク中立的 と解釈される。aの次数を大きくすると、例えば3にすれば分布の歪みの程度に対するリスク許容度も表現できる。
LPMの計算例
上記の準分散と同じ数値例を使う。
標本数Kは4でターゲット収益率は平均収益率0.0625とし、LPMの次数aは2に設定してみる。aの値を変化させればいろいろな次数のLPMが計算できる。

数式表示では

LPMに関する文献の中にはモーメントの次数aにゼロを認めているものがある。エクセルで計算するとゼロのゼロ乗 0^0 は#NUM!が返ってきて計算ができなくなる。統計ソフトRではゼロのゼロ乗は 0^0=1 となり1が返ってくる。ゼロ円投資してゼロ乗したら1円もらえたら夢のフリーランチになるが、数学的には何か奥深い理由がありそうだ。あまり詮索すると大変な泥沼に引き込まれそうなので、ゼロの近似値として0.001などを使うのが無難かもしれない。これならエクセルも問題なく計算してくれる。
LPMが下方リスクに着目した指標とすれば上方リスクに着目した指標も考えられる。それがUPMでる。
UPMは上方へのブレに着目した指標で。式で示せば以下のようになる。
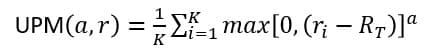
ショートポジションの投資家にとってみれば上方へ上振れることは文字通りリスクだろうが、通常のロングポジションを持つ投資家にとってはリスクではなく上方ポテンシャルを解釈される。ポートフォリオを編成するときにリスク回避的であっても上振れポテンシャルを一定水準以上に保って、その制約条件下で最小分散、最大収益を追求することも考えられる。
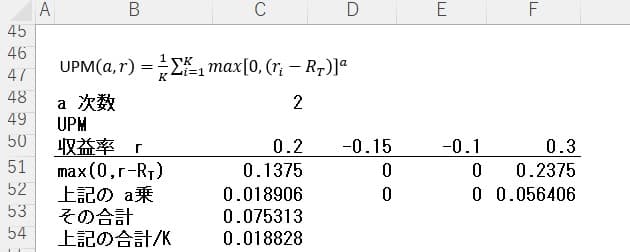
UPMの計算はエクセルの式をmax(0,RT-r) からmax(0,r-RT)
に書き換えるだけでよい。ターゲット収益率は平均収益率0.0625とし、LPMの次数aは2にUPMを計算すれば以下のようになる。
収益率分布の歪みとLPM、UPM
収益率の分布が歪んで偏っている場合にLPMとUPMがどのようになるか試算してみた。デリバティブの収益率の分布は正規分布にならず歪んでいるといわれているが歪んだt分布を使って右側に歪んだ(右方向にテールつまり尾っぽが長く伸びている分布,positive
skewnessとも呼ばれる)ケースと逆に左方向にテールが長く伸びている分布(negative
skewnessとも呼ばれる)のケースでシミュレーションを行ってみた。右方向に偏った分布は例えばOTMのオプション(コールやプットいずれでも)のロングやロング・ストラングルの時に見かける分布である。頻繁に損をすることが多いが、たまにボラティリティが急増したり大きなトレンドが発生するとオプション価格が高騰して過去の損失を取り返すようなパターンである。左方向に偏った分布はこれとは逆にOTMのオプションのショートやショートストラングルの時に見られる。こまめに小さな利益を得ることが多いが、たまにボラティリティが急増したり大きなトレンドが発生するとオプション価格が高騰して大きな損失をう受け過去の累積利益が消えてしまうパターンである。このskewed
t分布のグラフは以下のようになる。
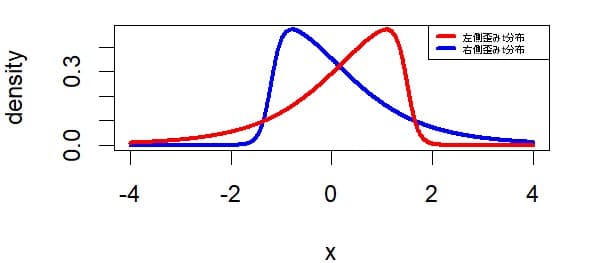
右側に歪んだt分布(青色のグラフ)のケース
右側に歪んだt分布の乱数を発生させ1万回のシミュレーションを行った結果、以下のような分布を得た。
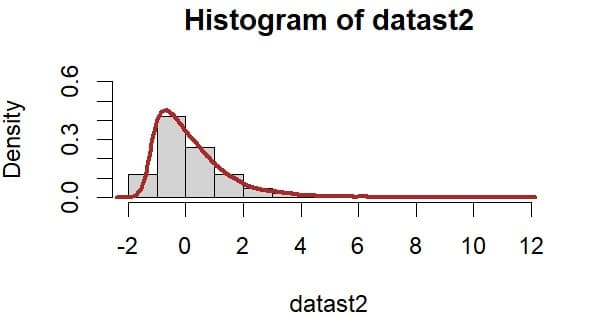
主な統計量をまとめると
収益率の範囲は
range(datast2)
-1.936587 11.686402
収益率の平均値は
mean(datast2)
0.2003327
収益率のメディアンは
median(datast2)
-0.1132417
収益率の標準偏差は
sd(datast2)
1.27604
収益率の尖度は
kurtosis(datast2)
6.039562
収益率の歪度は
skewness(datast2)
1.860004
歪度は右側に歪んでいることを示している。
収益率の平均値は0.2近辺だがメディアンは-0.11で容易には利益を稼得できないと予想できる。
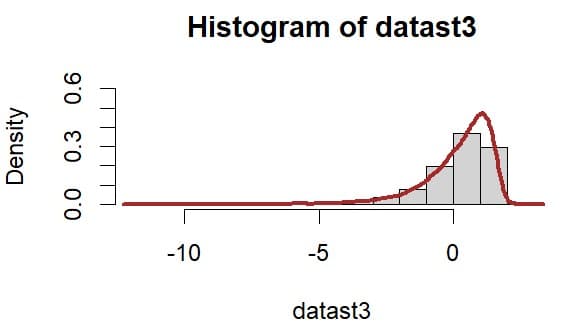
左側に歪んだt分布(赤色のグラフ)のケース
同様にして左側に歪んだt分布の乱数を発生させ1万回のシミュレーションを行った結果、以下のような分布を得た。
主な統計量をまとめると
収益率の範囲はrange(datast3)
-11.824511 2.871738
収益率の平均値は
mean(datast3)
0.1973851収益率のメディアンは
median(datast3)
0.519766収益率の標準偏差は
sd(datast3)
1.283855収益率の尖度は
kurtosis(datast3)
6.435739収益率の歪度は
skewness(datast3)
-1.922133
2つの事例は極端なケースかもしれないが収益率の平均値と標準偏差は同程度である。果たして投資家はどちらを選好するだろうか。
ターゲット収益率を平均収益率、モーメントの次数を2(投資家はリスク回避的)に設定して2つの分布についてLPMを計算してみると
右側(正の方向)に歪んだ分布の場合はLPM 0.48 左側(負の方向)に歪んだ分布の場合はLPM 1.2
と計算されるリスク回避的な投資家は右側(正の方向)に歪んだ分布を選好すると予想される。モーメントの次数3でLPMを比べると左に歪んだ分布の4.6に比べ、右に歪んだ分布は0.54と低いので、リスク回避的投資家は右に歪んだ分布を選好すると予想される。モーメントの次数を1に設定するとリスク中立的となりどちらの分布にLPMも0.47程度でほぼ同じになる。
同じ条件でUPMを計算すると右に歪んだ分布ではUPM
1.2 左に歪んだ分布ではUPM 0.47となり、右に歪んだ分布の方が上方ポテンシャルが大きいことを示している。
投資家自身がリスクに対してどのような許容度を持っているか、上昇ポテンシャルをどの程度好むのかなどは多分に感覚的、情緒的に認識されやすい傾向がある。これをLPMやUPMなどの指標を使い計数的に把握できれば投資家にとって好ましいポートフォリオがもっと具体的に描けてくるかもしれない。
拙文を書くのに使ったRコードは以下のとおり。パッケージsnは歪んだt分布の生成に、パッケージNNSはLPM,UPMの計算に,パッケージe1071 は歪度、尖度の計算のために利用した。
library(sn)
library(e1071)
library(NNS)
set.seed(123)
x= seq(-4,4, length=1000)
plot(x, dst(x, xi=-1.2,omega=1.5,alpha=8,nu=5),
ylab='density',
type ='l', col='blue',lwd=3)
lines(x, dst(x, xi=1.5,omega=1.5,
alpha=-8,nu=5), col='red',lwd=3)
legend("topright",
legend = c("左側歪みt分布","右側歪みt分布"),
lty=c(1,1),lwd=c(3,3),
col = c("red","blue"),cex=0.4)
set.seed(123)
datast2<-rst(n=10000, xi=-1.2, omega=1.5,
alpha=8,nu=5)
hist(datast2,freq=F,ylim=c(0,0.6))
lines(density(datast2),lwd=3,
col="brown",ylim=c(0,1))
range(datast2)
mean(datast2)
median(datast2)
sd(datast2)
kurtosis(datast2)
skewness(datast2) #右に歪んでいる
### right skewed
x<-datast2
LPM(0.01, mean(x), x)
LPM(1, mean(x), x)
LPM(2, mean(x), x)
LPM(3, mean(x), x)
#### UPM
## taeget=mean
UPM(0.01, mean(x), x)
UPM(1, mean(x), x)
UPM(2, mean(x), x)
UPM(3, mean(x), x)
#### left skewed
set.seed(123)
datast3<-rst(n=10000, xi=1.6, omega=1.5,
alpha=-8,nu=5)
hist(datast3,freq=F,ylim=c(0,0.6))
lines(density(datast3),lwd=3,
col="brown",ylim=c(0,1))
range(datast3)
mean(datast3)
median(datast3)
sd(datast3)
kurtosis(datast3)
skewness(datast3) #左に歪んでいる
x<-datast3
LPM(0.01, mean(x), x)
LPM(1, mean(x), x)
LPM(2, mean(x), x)
LPM(3, mean(x), x)
#### UPM
## taeget=mean
UPM(0.01, mean(x), x)
UPM(1, mean(x), x)
UPM(2, mean(x), x)
UPM(3, mean(x), x)
参考文献
Nawrocki, D. (1999) A Brief History of Downside Risk Measures. The
Journal of Investing