平均値の区間推定(財務分析への簡単な応用例)
Interval estimate of mean (application for financial analysis using Excel and R)
正規母集団(その母分散は未知)からサンプルを採り、その平均値の区間推定をすることがある。母分散が不明なので標本分散か不偏分散が代用されることになる。統計学のテキストでは標本分散を使うものもあれば不偏分散を使うものもある。最終的な結果は同じになるが、t統計量の設定の仕方が少し違ってくる。この辺が少し紛らわしいので簡単に整理してみた。最後に投資分析や財務分析での簡単な応用について検討してみた。なお、数学的な説明は統計学の専門サイトで解説されているようなので、ここでは単純な計算例で示すことにする。
ある正規母集団から4個のサンプルデータ
0.2
-0.15
-0.1
0.5
を得た。この4つのサンプルから母集団の平均値について区間推定をしてみる。平均値、分散、標準偏差などの計算はよく知られているので計算結果だけを表にしてある。

母分散を標本分散で代用する場合
95%の信頼区間を標本分散を使って推定してみる。
標本分散S2を使う場合は以下のように定義した統計量Tが自由度n-1のt分布に従うとされる。標準偏差Sが(標本数n-1)の平方根で除されていることが特徴になる。
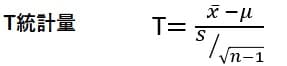
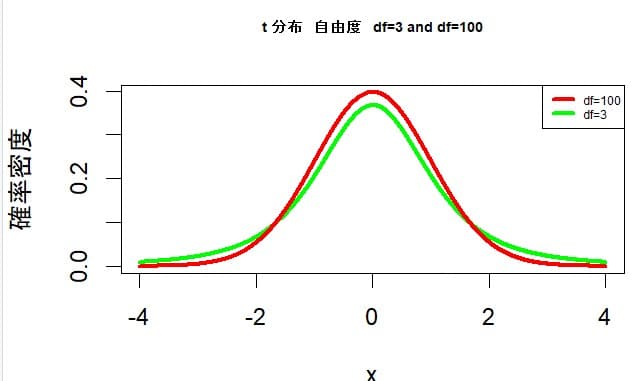
t分布では自由度nを無限大にすると正規分布に収束することが知られている。自由度100のt分布(赤色)は正規分布に近似しているが、自由度3のt分布(緑色)は正規分布に比べて両端部分が広がっている。(下図参照)
標本数が4なので自由度3(標本数4-1)で確率95%のt値をエクセルの関数T.INV()を使って求めてみる。
(統計ソフトRを使った計算例は文末にまとめてみた。)
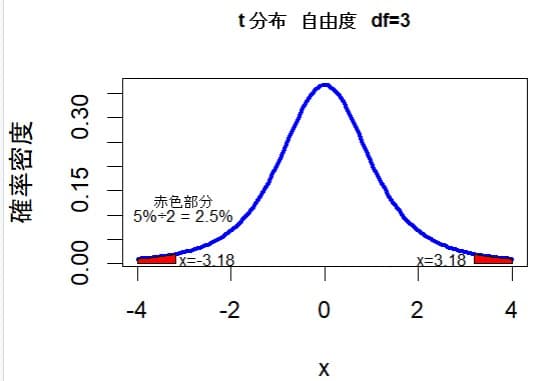
上図のようにt分布は左右対称なので5%の2分の1つまり2.5%の確率のt値を求めると
T.INV(0.025,3)=-3.1824
を得る。(上図の左側の赤色部分が2.5%になるようなxの値-3.182)同様にして97.5%の確率のt値を求めるとT.INV(0.975,3)=3.1824を得る。(上図の右側の赤色部分が2.5%になるようなxの値3.182) このように区間の下限を計算するときには-3.1824を使い、区間の上限を計算するときには3.1824を使うが、t分布は左右対称のグラフなので何れか一方が分かれば限度計算は出来る。3.1824を使って誤差を計算すると

従って信頼区間の下限と上限は次のようになる。
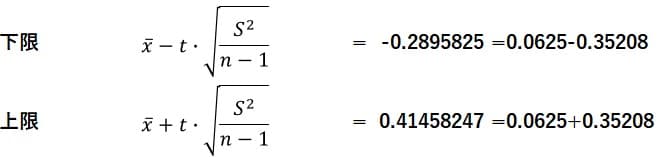
従って
信頼区間は(-0.2896, 0.4146)
となる。
母分散を不偏分散で代用する場合
次に信頼区間を不偏分散を使って推定してみる。
不偏分散U2を使う場合は以下のように定義した統計量Tが自由度n-1のt分布に従うとされる。標準偏差Uが標本数nの平方根で除されていることが特徴になる。
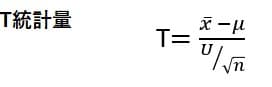
t値は3.1824と変わらないので下記のように計算すると同一の誤差0.352を得る。
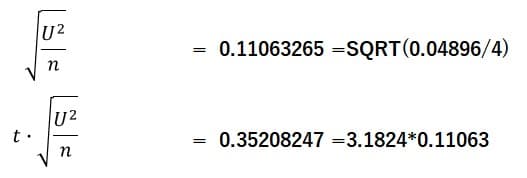
平均値0.0625に0.352を加減算すると
信頼区間は(-0.2896, 0.4146)
となる。母分散を標本分散で代用した場合と同じ結果になっている。
標本分散や不偏分散の式から偏差平方和を表せる。
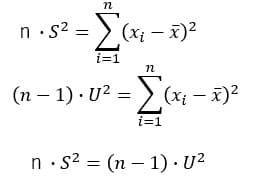
この関係式を使うと
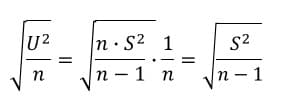
いずれの方式でも同一の誤差が計算できることが分かる。
財務分析、投資分析に対する簡単な応用例
投資信託などのパンフレットで、このファンドの過去の平均収益率は6.25%でリスクは19%などと示されていることがある。投資の収益率分布が正規分布に従うかどうかは専門家でも議論があるが、平均収益率の定義すら曖昧である。例えば前述の例の(0.2,-0.15,-0.1,0.5)を収益率と見立てれば平均収益率は6.25%になる。これは(0.2,-0.15,-0.1,0.5)の合計をサンプル数4で除したものである。
別のアプローチとして投資資産の4年間の平均的な成長率を幾何平均で考えれば
(1+0.2)*(1-0.15)*(1-0.1)*(1+0.5)=1.1934
この4乗根 1.1934(1/4)
=1.04519
となる。
このような幾何平均で平均収益率を考えると4.519%となり算術平均の6.25%よりも低い数値となる。算術平均の収益率だと過大な期待を持たせるかもしれない。しかし通常は平均値がどのように算出されたかは不明なので、たぶん算術平均なのだろうと推測するしかない。もしリスク指標の基となっている分散が不偏分散か標本分散かが分かり、しかもサンプル数n(ここでは平均の年数)が分かれば平均収益率の区間推定が可能となる。通常はこのようなデータは不明なので残された手段は自己勝手流に山勘で推測することになる。例えば、平均収益率6.25%、リスク19%と示されていたする。詳細は不明なので、山勘で平均年数は4年で標本分散に基づくリスクと仮定すれば、上記で計算したように平均収益率の信頼区間は
(-0.2896, 0.4146)と計算できる。投資信託についてはシャープレシオが開示されているケースが多いが、その場合には平均年数nが開示されていればそれを使い、開示されていなければ例えば5年とか自分の好みで仮定することにより区間推定的(推定もどきの)な計算が可能となる。あくまで自己責任となるが工夫次第で様々な計算が楽しめるだろう。
統計ソフトRによるコードの1例
x<-c(0.2,-0.15,-0.1,0.3) # 標本
mean(x) # 標本平均値
samplevar<-var(x)*(length(x)-1)/length(x)
samplevar # 標本分散
unbiasvar<-var(x)
unbiasvar # 不偏分散
x <- seq(-4, 4, by=1/1000)
plot(x, dt(x, 100), type="n", xlab="x",
ylab="確率密度")
title("t 分布 自由度 df=3 and df=100",cex.main=0.8)
lines(x , y = dt(x, df = 3), lwd = 3, col =
'green')
lines(x , y = dt(x, df =100), lwd = 3, col =
"red")
legend("topright", legend = c("df=100","df=3"),
lty=c(1,1),lwd=c(3,3),
col = c("red","green"),cex=0.5)
plot(x, dt(x, 3), type="n", xlab="x",
ylab="確率密度")
title("t 分布 自由度 df=3",cex.main=0.8)
curve(dt(x, 3), type="l",lwd=3,col="blue" ,add=T)
text(-2.5,0.01,"x=-3.18",cex=0.7)
xgl<-seq(-4,-3.18,length=100)
ygl<-dt(xgl,3)
polygon(c(xgl,rev(xgl)),c(rep(0,100),rev(ygl)),col="red")
xgr<-seq(3.18,4,length=100)
ygr<-dt(xgr,3)
polygon(c(xgr,rev(xgr)),c(rep(0,100),rev(ygr)),col="red")
text(2.5,0.01,"x=3.18",cex=0.7)
text(-3,0.13,"赤色部分",cex=0.7)
text(-3,0.1,"5%÷2 = 2.5%",cex=0.7)
## 母分散を標本分散で代用する場合
t0975df3<-qt(0.975,3)
t0975df3
gosasv<-t0975df3*sqrt(samplevar/(length(x)-1))
gosasv # 誤差部分の計算
lowersv<-mean(x)-gosasv #信頼区間下限
lowersv
uppersv<-mean(x)+gosasv #信頼区間上限
uppersv
#####################
## 母分散を不偏分散で代用する場合
gosaun<-t0975df3*sqrt(unbiasvar/length(x))
gosaun
lowerun<-mean(x)-gosaun
lowerun
upperun<-mean(x)+gosaun
upperun