エクセルで資本市場線（CML)と市場（マーケット）ポートフォリオ

注記
以下の文はＥｘｃｅｌ２０１３を使用して書かれている。最新のバージョンExcelでは行列演算が動的配置のため若干操作が異なるかもしれない。下記中段の「添付されたテキストファイル利用法」を参照されたい。

２つのリスク資産、例えば株式A、株式Bから成るポートフォリオの効率的フロンティアはマーコヴィツ(Markowitz)の方法で計算できる。マーコヴィツによれば、投資家はリスク回避的で、しかも、一定のリスク（標準偏差）のもとで最大の収益率を追求すると仮定すれば、単独の株式より多数の株式をうまく組み合わせて運用するほうが合理的である。このときポートフィリオの収益率とリスク（標準偏差）の関係は双曲線で表せる。特に、その双曲線の上半分の部分は効率的フロンティア呼ばれている。２銘柄ポートフォリオの効率的フロンティアの計算例は空売り許容ポートフォリオの効率的フロンティアで取り扱っているので、ここでは株式のようなリスク資産の他に無リスク資産（安全資産とも呼ばれる）、例えば貸付金が資産運用の選択肢に加えられたと仮定する。このような場合に、リスク回避的で合理的な投資家はどのような資産選択をするだろうか。最もリスク回避的な投資家は無リスク資産１００％の運用を選び、ややリスク許容度が高い投資家はリスク資産ポートフォリオと貸付の組合せを選択し、もっとリスクを負担できると考える投資家はマイナスの貸付、つまり借入をしてその資金と自己資金を合わせてリスク資産ポートフォリオに投資するだろう。ここで、リスク回避的な投資家にとってはA株と貸付、あるいはB株と貸付という組合せは選択しない。なぜならA株単独の保有より２銘柄のポートフォリオのほうが分散投資効果でリスクが低くなるのでリスク資産ポートフォリオの効率的フロンティア上の適当なポートフォリオを選択する。では、その適当なポートフォリオをどのようにして見つけるかというのが問題となる。理論的に突っ込んだ話は多くのファイナンスのテキストに書かれているので、ここではA株とB株の2株式だけで、投資家は何時でも２％の金利で借入や貸付が可能な世界を想定した簡単な設例を使って計算実験を行ってみる。
A,B各株式の収益率、標準偏差、共分散は下記のようだとする。

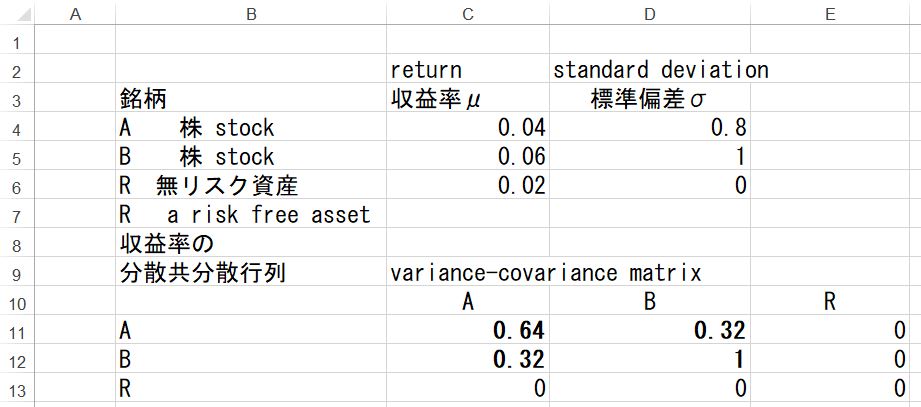
資本市場線と市場ポートフォリオ

まずリスク資産である株式ポートフォリオの効率的フロンティアを計算すると下記のようになる。計算方法は　空売り許容ポートフォリオの効率的フロンティア　を参照されたい。

無リスク資産が追加された場合の効率的フロンティアは下図のようになる

資本市場線グラフ
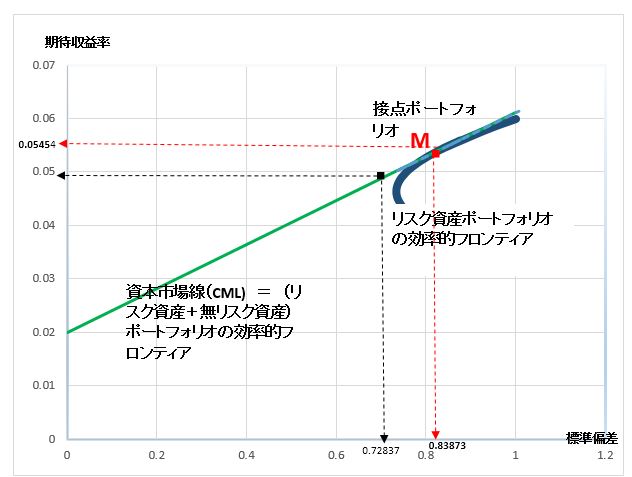
資本市場線と市場ポートフォリオ

青色の双曲線は株式2銘柄から成るリスク資産ポートフォリオの効率的フロンティアを示している。無リスク資産の収益率０．０２を切片として効率的フロンティアに接する緑の直線が資本市場線となる。リスク資産に無リスク資産（安全資産）が加わってくると、双曲線でなく、この緑色の資本市場線が効率的フロンティアに変わってくる点に注目すべきである。グラフ上ではMのところで直線が双曲線に接しており、このMを接点ポートフォリオ呼んでいる。緑色の資本市場線は一定のリスク（標準偏差）のもとでは最大の収益率を示す線となっており、投資家はこの線上で無リスク資産と接点ポートフォリオMの組み合わせを選ぶことになる。

接点ポートフォリオの計算(finding tangent portfolio)

株式A、Bおよび無リスク資産Rへの投資比率（ウエート）を
W_A、W_B,　W_R　で表す。各資産の収益率はμ_A、μ_B、μ_R
リスク資産と無リスク資産を含む全体のポートフォリオの収益率はμ_P
各資産の標準偏差をσ_A、σ_B、σ_R、
株式AとBの共分散はσ_AB
リスク資産と無リスク資産を含む全体のポートフォリオの標準偏差σ_P　。
なお、無リスク資産の収益率は０．０２は定数でバラツキはないので、その標準偏差や他の資産との共分散はゼロとなる。(As a risk free asset's return is constant,it has no variance and no covariance)

以下に示すような制約条件の下でポートフォリオ全体の分散を最小化するための投資比率を求めることになるが、これは条件付極値問題となる。これはラグランジュ関数を各変数で偏微分すると連立方程式が導け、これを解くことで最適な投資比率が計算できる。。

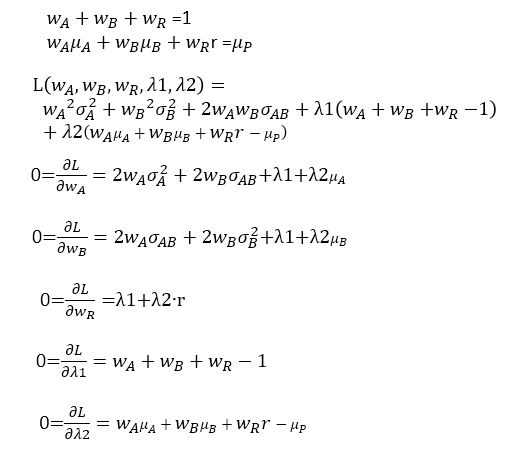
リスク資産と無リスク資産の全体から成るポートフォリオの目標収益率を仮に５％とおいて連立方程式を解くと以下のようになる。エクセルの行列演算によるポートフォリの計算については　エクセルで簡単な行列演算（３資産ポートフォリオ分析のために）　　を参照されたい。連立方程式で緑色の範囲が係数行列でピンクの部分は定数ベクトルを示す。係数行列の逆行列に定数ベクトルを乗じることで解が得られる。

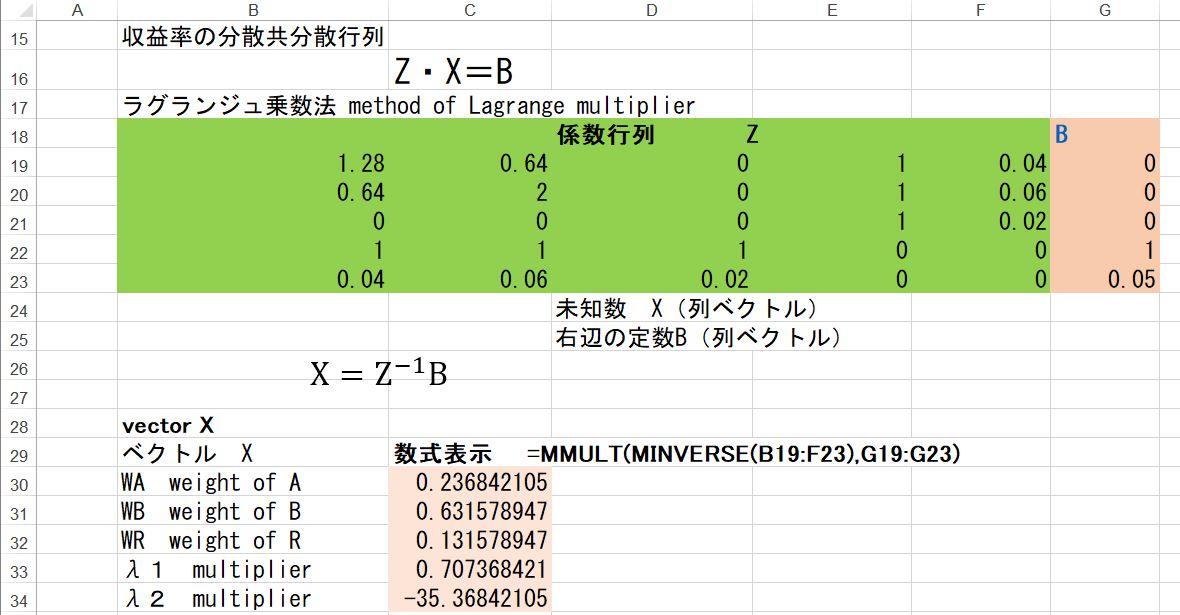
W_A+W_B+W_R=0.23684+0.63158+0.13158 ＝１　　から、リスク資産だけのポートフォリオ　の投資比率の計算は以下のようになる。

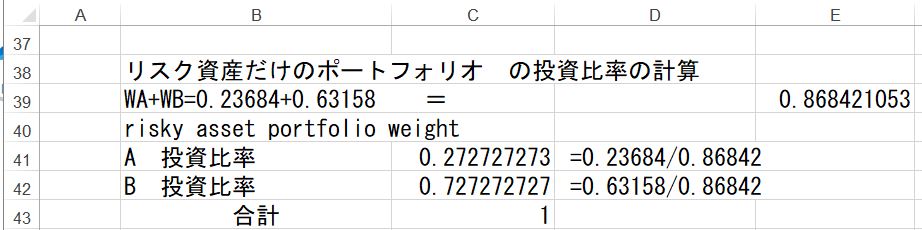
これが接点ポートフォリオの投資比率となる。この投資比率を使って接点ポートフォリオMの期待収益率と分散等を求めると以下のようになる。

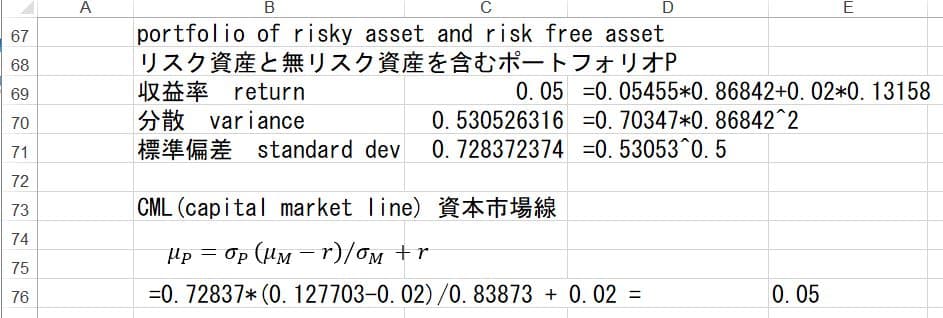
リスク資産と無リスク資産を組み合わせたポートフォリオの収益率と分散は以下のように計算できる。W_A+W_B+W_R=0.23684+0.63158+0.13158 ＝１　　から、
無リスク資産の投資比率は０．１３１５８、従ってリスク資産への投資比率は１－０．１３１５８＝０．８６８４２となるので

--------------------------------

添付されたテキストファイルpflinedata.txtの利用法

このテキストファイルを開いて全てを選択(Ctl + a)してコピーしExcelの新しいシートのセルA１にそのまま貼りつければ計算例のワークシートが再現できる。(Excel2016以降であれば可能、それより以前のversionではセルの分割作業が必要かもしれない）
具体的な手順は以下のとおり
１　このテキストファイルを開く
２　すべてテキストを選択する(Ctl + a)
３　Excelの新しいシートのセルA１に貼りつける

行列演算の部分は＃スピル(spill) と表示されるがもしれないが、セルC30-C34の＃スピル！と表示されている部分を選択しF2 キーを押して、次に Ctrl+Shift+Enter で確定さすと計算結果が得られる。この文を書いた時にはExce l　2013を使っていたが最近のバージョンでは動的配列で行列演算するようで＃スピル(spill) が出てしまう。各自で工夫して適当に修正して頂きたい。行列演算以外の基本的データは再現できると思う。
To recreate the example worksheet, open this text file, select everything (Ctrl + a), copy it, and paste it directly into cell A1 of a new Excel sheet. (This is possible in Excel 2016 and later; earlier versions may require splitting cells.)
The specific steps are as follows:
1. Open this text file.
2. Select all text (including blank spaces).
3. Paste it into cell A1 of a new Excel sheet. The matrix operations may display #spill, but you can get the results by selecting the #spill! section in cells C30-C34, pressing F2, and then pressing Ctrl+Shift+Enter to confirm. I was using Excel 2013 when I wrote this, but recent versions seem to use dynamic arrays for matrix operations, resulting in #spill. Please modify this as needed. I believe you can recreate basic data other than matrix operations.
ワークシートでなくテキストファイルを添付した理由などについてはエクセルのワークシートをテキスト化して簡単に通信
を御参照
--------------------------------

資本市場線(capital market line)

この資本市場線をグラフにすれば緑色の直線になる。

資本市場線の算式は下記のようにして求める。μ_Pはリスク資産と無リスク資産から成るポートフォリオの収益率、その標準偏差をσ_P,接点ポートフォリオの収益率をμ_M、その標準偏差をσ_M、ｒは無リスク資産収益率、αは無リスク資産の投資比率(proportion invested in risk free asset)、接点ポートフォリオの投資比率は1-α(proportion invested in tangent portfolio)で表すと下記のように１－αはσ_P/σ_Mとなるので、それをμ_Pの式に代入して整理すると得られる
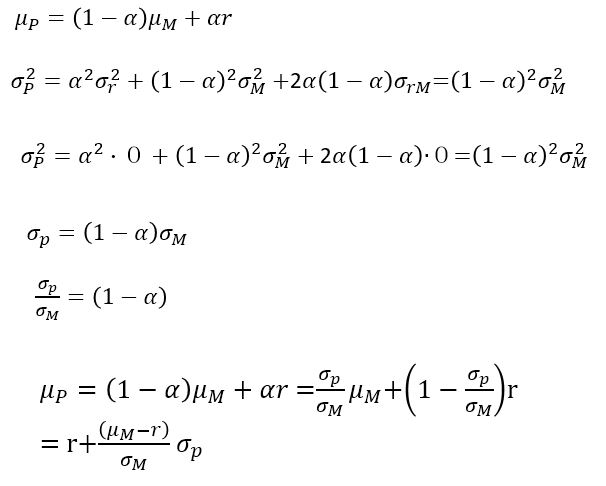
i資本市場線

μ_P＝（1-α）μ_M＋αｒ　の算式でαを－２から１まで変化させると以下のようになる。

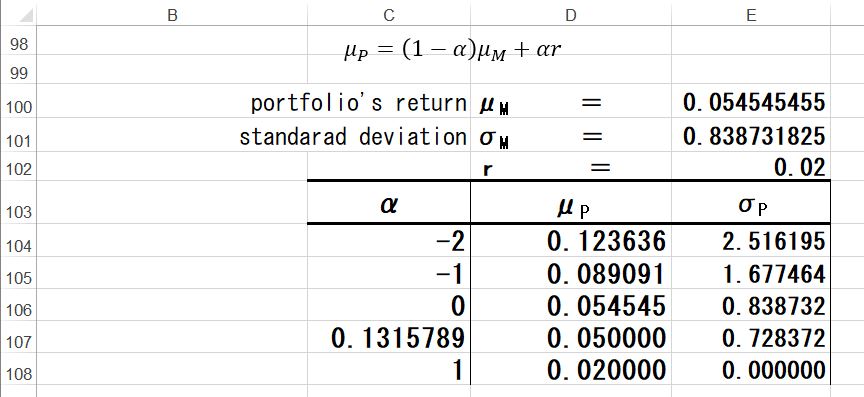
αがマイナス２ということは２％の利子率を支払って借入を行い、その資金と自己資金を加えて接点ポートフォリに投資するといったレバレッジを効かしたポートフォリオで収益率１２．４％標準偏差２５１％になる。収益率は大きくなるがそれに伴いリスク（標準偏差）も非常に大きくなっている。α＝０は接点ポートフォリオそのもので、収益率５．４５４５％、標準偏差７３％となり、α＝１は無リスク資産だけのポートフォリオになるので収益率２％標準偏差はゼロとなっている。

ここまではリスク回避的な個別の投資家の立場としては無リスク資産が存在する場合にはリスク資産のポートフォリオとして接点ポートフォリオを選択することが最適という結論に至ったが、もし、全ての投資家が同様の行動をとった場合に市場全体はどのような均衡状態になるのかを考えることにする。
　市場全体で考えるときには、全ての投資家は期待収益率や分散、共分散など同一の予想をするという同質的期待の仮定を前提とする。自分も隣人も話題のセレブも皆同じ情報を入手し同じように分析し数理計画法を使ってA株とB株への投資比率を計算する。その場合には全ての投資家は投資金額の大小は異なっても接点ポートフォリオを選択するのでリスク資産の投資比率は接点ポートフォリオの投資比率で同一となる。この時に国勢調査のような形で各投資家のポートフォリオを調査して集計すれば、結局、各個人の接点ポートフォリオを集計することになる。経済全体ですべての投資家が保有するリスク資産を合計したものを市場（マーケット）ポートフォリオと定義すれば、均衡状態での市場ポートフォリオはすべての投資家が保有する接点ポートフォリオを総合計したものに等しくなる。２株式だけの世界で考えると、市場で需給が均衡して均衡価格が成立している状態では、各株式の発行済株式数×時価（均衡価格）を集計したポートフォリオの総額が市場ポートフォリオになる。

2銘柄4人投資家の仮想市場(Virtual stock market composed of 2 stocks and 4 investors)

　A、Bの２銘柄の株式（リスク資産）しかなく、投資家も自分、その隣人、金持ち、超金持ちの４人しかいない世界での市場ポートフォリオのイメージを表にすると以下のようになる。

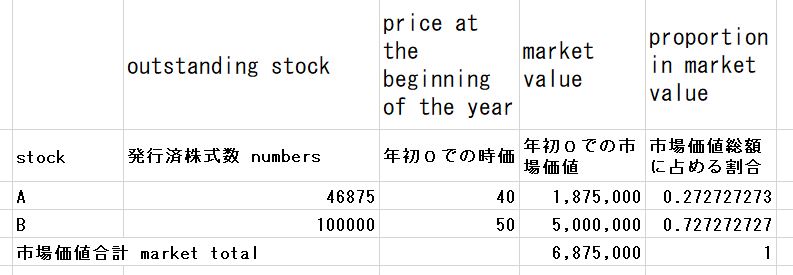
仮想証券市場

年初０時点で市場で需給が均衡している状態での市場ポートフォリオは6,875,000 となる。市場ポートフォリオの銘柄別の市場価値の構成割合は

	市場価値総額に占める割合
A	0.272727273
B	0.727272727
合計	1

となって接点ポートフォリオの投資比率と等しくなっている。
これを投資家別のポートフォリオの内訳で見ると以下のようになる。

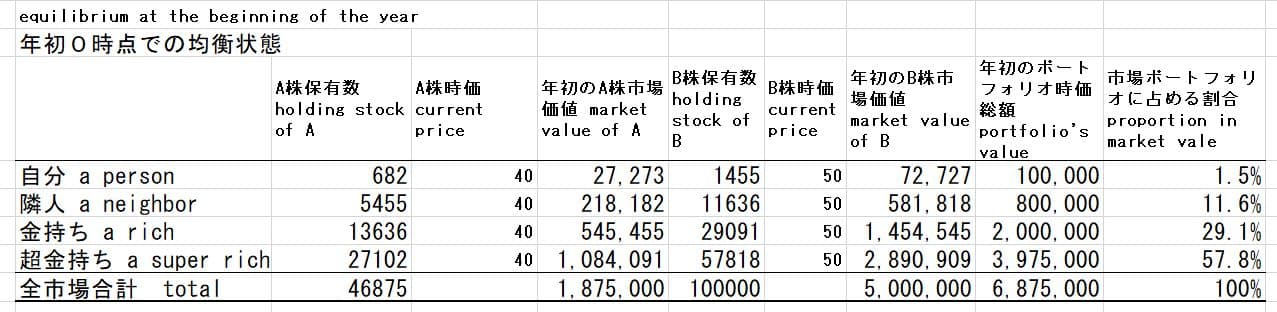
投資家別市場ポートフォリオ保有状態

株式2銘柄、4人の投資家からなる仮想世界での市場（マーケット）ポートフォリオは市場価値総額で6,875,000でA株1,875,000、B株5,000,000で構成されているこの市場ポートフォリオのA株構成割合は1875000／6875000＝０．２７２７３と接点ポートフォリオのA株へと投資比率と同じになっている。

同質的予想や完全市場などの仮定の下で市場均衡が成立している場合には
均衡状態で各投資家は市場ポートフォリオの一部を保有していると考えられる。このため接点ポートフォリオと市場ポートフォリオを同義に使って説明が行われることも多い。市場ポートフォリオは集計値の性質が大きいと思われるが、各投資家の接点ポートフォリオを市場ポートフォリオと呼ぶことも多い。例えば上記の表で自分投資家は１００，０００の接点ポートフォリオを保有するが、市場ポートフォリオの１．５％を保有していることにもなるので、自分投資家は市場ポートフォリオを持っていると言われる。市場全体で考えるとき、市場が均衡していれば資本市場線グラフも同様のグラフとなる。そこで接点ポートフォリオを市場ポートフォリオと読み替えれば
μ_P＝σ_P（μ_M－ｒ）／σ_M＋ｒ　の資本市場線で　（μ_M－ｒ）／σ_Mの部分をリスクの市場価格と呼んだりする。

ファイナンスや金融経済学のテキストでは同質的予想、リスク回避的投資家、無限小の単位で取引可能といった幾つかの仮定をおいて、精緻な理論展開をして一定のモデルを導出している。非常に難解な世界に見えるので筆者は勉強したことはないが興味のある人は金融経済学(financial economics)の専門書を参照されたい。

財務入門目次へ