ブートストラップ(empirical bootstrap)法 Rによる初歩的、入門的計算例
This presents an elementary introduction to
empirical bootstrap using simple R code examples.
ブートストラップ法は1つの初期標本から重複(反復、復元)を許可して疑似標本(ブートストラップ標本)を生成しブートストラップ分布を得て、そこから平均値等の標本統計量の誤差やバラツキなどの分析、評価をする方法をいう。このブートストラップ法は何か新しい画期的な推定値を教えてくれるわけではないが、標本統計量の精度などを評価するための情報を提供してくれる。一般的に統計的な推測をするとき未知の母集団の特性を調るために無作為標本抽出をして平均値とか分散といった統計量の標本分布を理論に基づいて分析し、その推定値やその誤差など評価する。よく知られている標準誤差は、一般的には標本平均値の標準偏差を意味することが多いが、もっと広い意味で統計量の標準偏差を指すこともある。この標準誤差は推定値の精度とか信頼度の指標として使われている。よくテキストで出てくる例題で、例えば一組の無作為抽出で得られた1組のサンプル(a
sample)
(69, 46, 88 ,54, 66,
30)があるとする。サンプルサイズは6で小さいがこの標準誤差はサンプルの標準偏差をサンプルサイズの平方根で除して求める。エクセルの関数STDEV.S()を使って不偏標準偏差を計算すると20.1238を得る。従って標本平均の標準誤差は20.1238÷√6 ≒ 8.2155 と計算される。Rで計算すると以下のようになる。
x<-c(69, 46, 88 ,54, 66, 30)
#初期サンプル
nx<-length(x) #サンプルサイズ
nx
## [1] 6
mean(x)
サンプル平均(標本平均のブートストラップでは初期サンプルの平均値は母集団の平均値として代用される)## [1] 58.833
var(x)
## [1] 404.97
(var(x))^0.5
## [1] 20.124
sd(x) #サンプルの不偏標準偏差
## [1] 20.124
#標準誤差
sd(x)/nx^0.5 #標本平均の標準誤差
## [1] 8.2155
しかし、たった1組のサンプルしかないのに何で標準偏差が計算できたのか疑問に思う人もいるだろう。仮にサンプル組数が10個であれば各組サンプルの標本平均値を求め10個の標本平均からその分散や標準偏差を求めることは理解できるが1組の標本で標本平均の標準偏差が計算できるのは不思議に見える。これには訳があり理論から得られた算式に基づいて標本誤差を計算している。その理論とは何かといえば中心極限定理という有名な定理がある。この定理によれば標本サイズnが大きくなると標本平均の分布は母平均μ、分散σ2/n の正規分布近づくことが証明されている。これを利用して標本平均の標準偏差を分散σ2/nから求めている。もちろん母集団の母平均μ、分散σ2 は未知であるが1組のサンプルから得られた推定値を代用して設例のように算式 σ/√nに代入して計算することになる。もし無作為抽出で得られた1組のサンプル(標本は互いに独立で同一の分布 iidに従うとする)が未知の母集団の特性を反映し十分に母集団を代表しているとすれば、このサンプル(初期標本と呼ぶ)を基にして
重複(反復、復元)を許可してブートストラップ標本を生成し、そこから平均値等の統計量のブートストラップ分布を得れば、それは本来の標本分布に近似していると考えられる。このようにブートストラップ分布を母集団から得られた標本分布、初期標本を母集団の役割を果たすものと見立てて推定量の精度に関する情報を得ようとするものである。ブートストラップ標本から計算した統計量の変動は本来の標本統計量の変動と近似していると考えられるのでブートストラップ分布の形状(例えば釣鐘状かどうか)、分布の中心が初期標本から得た統計量(例えば平均値)に近いか、バラツキ、標準偏差などを調べることで統計量の精度や信頼区間などの情報を得ることが出来る。なお上記のようなブートストラップ法をempirical
bootstrap 、nonparametric bootstrap あるいは Efron's bootstrap などと呼ばれている。
具体的な計算例でないと分かりにくいので、先ほどの標本平均の標準誤差の計算で使ったサンプルでブートストラップ標本平均と標準偏差を計算してみる。
初期標本(original sample of size = 6)は(69, 46, 88 ,54, 66, 30)。サンプルサイズが6なので同じサイズのサンプルを10個生成してみる。(We
make 10 resamples from this original sample,with replacement.)
x=(69(1)、46(2),88(3),54(4)、66(5)、30(6))初期標本の上付き文字(1)などはデータの順番を示すインデックスとする。サンプルサイズが6なので1から6番までのインデクスを付ける。ブートストラップ法では具体的には整数1から6までの数から重複(反復)を許可して一様乱数を発生させる。例えば1回目のサンプリングで(3、6、3、2.2、6) という乱数を得たなら、この整数に対応する
xのインデックスを持つデータがサンプルとして選ばれる。xの3番目のデータは88、6番目のデータは30、3番目のデータは88
、2番目のデータは46、2番目のデータは46、6番目のデータは30 となり(88、30,88、46、46,30)といったブートストラップ
サンプルができる。Rの計算例では以下のようになる。(We have one original sample of 6 observations.
Then we create 10 resamples by sampling with replacement. The original
sample are treated as if it were a real population. We try to find the
bootstrap distribution of the mean and its standard error.)
set.seed(123)
sample(1:6, replace = T)
## [1] 3 6 3 2 2 6
#このような作業をsample(x, replace = T)
で行うと
set.seed(123)
sample(x, replace = T)## [1] 88 30 88 46 46 30
このような反復(復元)サンプリングを繰り返すことで独立した同一分布(iid)のサンプルが多数生成でき、このような作業をsample(x, replace = T)で行っている。
以下ではサンプリングを10回行い10組のサンプルを生成している。このブートストラップ標本を使って標本平均の平均値を計算してみる。シミュレーション回数は10回と小さいが、このほうが原始的になるがプログラムの流れを肉眼で追跡するのに好都合である。(Though
10 resamples are a very few,it is convenient for code tracing and debugging)プログラムの書き方は様々にあると思うが初歩的な書き方A法からD法までの4つで比較してみた。最後のD法はブートストラップ専門のパッケージbootを利用する。
4通りのシミュレーション(4 resampling methods)
初期サンプル(original sample) (69, 46, 88 ,54, 66, 30) はブートストラップ法では母集団と見なされ、この初期標本を基にして反復(復元)サンプリングで独立した同一分布(iid)のサンプルが生成される。シミュレーションA(resampling method A)
for loopを使って復元サンプリングする方法である。zが標本平均10個からなるベクトルとなる。以下のRでの計算のように偏り(バイアス) 2.8833となっている。
x<-c(69, 46, 88 ,54, 66, 30)
#初期サンプル
z<- vector() # ベクトルを準備する
nsims<-10 #シミュレーション回数の設定
set.seed(123)
for(i in 1:nsims){
bootm <- sample(x, replace = T)
print(bootm)
z[i] <- mean(bootm)
}
#10組のブートストラップサンプルが生成される
## [1] 88 30 88 46 46 30
## [1] 88 66 54 30 30 69
## [1] 46 88 66 88 88 69
## [1] 54 69 69 66 88 46
## [1] 46 69 30 88 54 30
## [1] 69 88 66 54 46 66
## [1] 69 69 46 88 54 66
## [1] 66 88 30 69 46 66
## [1] 66 54 66 46 69 69
## [1] 88 69 30 66 69 46
z
#各ブートストラップサンプルの標本平均
## [1] 54.667 56.167 74.167 65.333 52.833 64.833 65.333 60.833 61.667
## [10] 61.333mean(z) #標本平均の平均値
## [1] 61.717
sd(z) #標本平均の標準誤差
## [1] 6.247
mean(z)-mean(x) #偏り(バイアス)
## [1] 2.8833
シミュレーションB(resampling method B)
ブートストラップサンプルを(サンプルサイズ X
シミュレーション回数)だけ生成し、それを列方向(右方向)に行列変換して1列が1個のブートストラップサンプルとしている。結果はシミュレーションAと同一となる。
set.seed(123)
tmpdata1 <- sample(x,nx*nsims, replace=T)
tmpdata1
## [1] 88 30 88 46 46 30 88 66 54 30 30 69 46 88 66 88 88 69 54 69 69 66
## [23] 88 46 46 69 30 88 54 30 69 88 66 54 46 66 69 69 46 88 54 66 66 88
## [45] 30 69 46 66 66 54 66 46 69 69 88 69 30 66 69 46これはfor loop プログラムで作成したブートストラップサンプルと同一になっている。
bootsp1 <- matrix(tmpdata1, nrow=nx, ncol=nsims,byrow=F)
bootsp1
## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
## [1,] 88 88 46 54 46 69 69 66 66 88
## [2,] 30 66 88 69 69 88 69 88 54 69
## [3,] 88 54 66 69 30 66 46 30 66 30
## [4,] 46 30 88 66 88 54 88 69 46 66
## [5,] 46 30 88 88 54 46 54 46 69 69
## [6,] 30 69 69 46 30 66 66 66 69 46
各列の平均値が標本平均のブートストラップサンプル
xbarm1 <- colMeans(bootsp1)
以下のような標本平均のブートストラップ標本10個を得る
xbarm1
## [1] 54.667 56.167 74.167 65.333 52.833 64.833 65.333 60.833 61.667
## [10] 61.333これはfor loop プログラムでの結果と
同一になっている。
mean(xbarm1) #標本平均の平均値
## [1] 61.717
sd(xbarm1) #標本平均の標準誤差
## [1] 6.247
mean(xbarm1)-mean(x) #偏り(バイアス)
## [1] 2.8833
シミュレーションC(resampling method C)
基本的にはB法と同じだがブートストラップサンプルを(サンプルサイズ X
シミュレーション回数)だけ生成し、それを行方向(下向き)に行列変換している。そのため計算結果はB法とは微妙な差が出ている。シミュレーション回数が増えれば無視できる差異になるだろう。
bootsp2 <- matrix(tmpdata1, nrow=nx, ncol=nsims,byrow=T)
各列の平均値が標本平均のブートストラップサンプル
bootsp2
## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
## [1,] 88 30 88 46 46 30 88 66 54 30
## [2,] 30 69 46 88 66 88 88 69 54 69
## [3,] 69 66 88 46 46 69 30 88 54 30
## [4,] 69 88 66 54 46 66 69 69 46 88
## [5,] 54 66 66 88 30 69 46 66 66 54
## [6,] 66 46 69 69 88 69 30 66 69 46上記の2つのシミュレーションによる結果とはブートストラップサンプルの並べ方が異なるので若干であるが標準誤差が異なっている。シミュレーションの回数が多くなれば無視できるだろう。
xbarm2 <- colMeans(bootsp2)
xbarm2## [1] 62.667 60.833 70.500 65.167 53.667 65.167 58.500 70.667 57.167
## [10] 52.833mean(xbarm2) #標本平均の平均値
## [1] 61.717
sd(xbarm2) #標本平均の標準誤差
## [1] 6.3026
mean(xbarm2)-mean(x) #偏り(バイアス)
## [1] 2.8833
シミュレーションD(resampling method D ,using package "boot")
パッケージbootを使うのでプログラムは簡潔になる。だたブートストラップサンプルから標本平均を計算する関数を自作する必要がある。この場合サンプリング用のインデックスを引数に与えるよう作る必要がある。シミュレーションAのfor
loop での i に相当するインデックスが必要となる。
################# boot #########
zz<- vector() # ベクトルを準備する
suppressMessages(library(boot))
boot.mean <- function(x,i){
boot.mean <- mean(x[i])}
set.seed(123)
zz <- boot(x,boot.mean, R = nsims)
mean(zz$t) #標本平均の平均値
## [1] 61.717
sd(zz$t) #標本平均の標準誤差
## [1] 6.3026
mean(zz$t)-mean(x) #偏り(バイアス)
## [1] 2.8833
bootではどのようなサンプリングをしたか調べてみる。ba1<-boot.array(zz, indices = TRUE)
ba1
## [,1] [,2] [,3] [,4] [,5] [,6]
## [1,] 3 6 1 1 4 5
## [2,] 6 1 5 3 5 2
## [3,] 3 2 3 5 5 1
## [4,] 2 3 2 4 3 1
## [5,] 2 5 2 2 6 3
## [6,] 6 3 1 5 1 1
## [7,] 3 3 6 1 2 6
## [8,] 5 1 3 1 5 5
## [9,] 4 4 4 2 5 1
## [10,] 6 1 6 3 4 2
例えば、1行目のインデックスは(3, 6, 1, 1, 4, 5)が抽出されているので1回目のサンプルは初期サンプルxの対応インデックスのデータは (88, 30, 69, 69, 54, 66) であることが分かる。これはシミュレーションCで得たbootsp2の第1列と同じ数値となっている.標準誤差の計算結果もシミュレーションCと同一となっている。
ライブラリーのbootでは出力結果で比較してみるとシミュレーションCと同じようなサンプリングをしているのかもしれない。(Judging from the
result, "boot" may resample by using a similar way of method C.)
シミュレーションの回数10,000の場合
(case of 10 thousand resamples)
シミュレーションC(using resampling method C)の方法でシミュレーション回数を10,000にしてブートサンプルの分布がどのような形になるか調べることにする。
set.seed(123)
nsims<-10000
tmpdata3 <- sample(x,nx*nsims, replace=TRUE)
bootsp3 <- matrix(tmpdata3, nrow=nx, ncol=nsims,byrow=T)
xbarm3 <- colMeans(bootsp3)
mean(xbarm3) #標本平均の平均値## [1] 58.866
sd(xbarm3) #標本平均の標準誤差
## [1] 7.5217
mean(xbarm3)-mean(x) #偏り(バイアス)
## [1] 0.032267
偏り(バイアス Bias)=ブートストラップ標本平均-標本平均(初期サンプルの平均値)は小さいので統計量の精度は高そうに見える。
以下ではバイアスのベクトルからバイアス(偏り)の分布を求め、そこから信頼区間を計算してみる。
delta1 <- xbarm3 - mean(x)
hist(delta1,prob=T)
abline(v = mean(delta1),lwd=3)
lines(density(delta1,kernel="gaussian",
lwd=3,col="red")
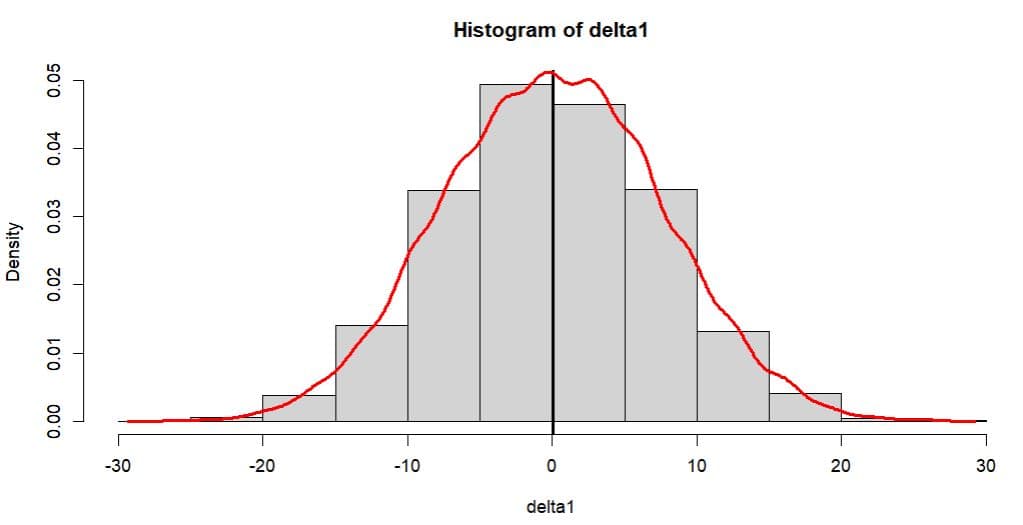
バイアス(偏り)のブートストラップ分布(経験分布)からquantile()で80%信頼区間を計算してみる。

d = quantile(delta1,c(0.1,0.9))
cr<-seq(0,1,0.05)
dd<-quantile(delta1,cr)
dd
## 0% 5% 10% 15% 20% 25% 30%
## -26.16667 -12.33333 -9.66667 -7.83333 -6.50000 -5.16667 -4.00000
## 35% 40% 45% 50% 55% 60% 65%
## -3.16667 -1.83333 -0.83333 0.00000 1.00000 2.00000 3.00000
## 70% 75% 80% 85% 90% 95% 100%
## 4.00000 5.16667 6.33333 7.83333 9.66667 12.50000 26.00000
バイアスθの80%信頼区間
θ^-θの分布のα、1-αの分位点wa、w1-a
(θ^-w1-a θ^-wa)はθの100(1-2α)%の信頼区間となるのでαは0.1となり下記のように計算できる。θ^は初期標本の平均値mean(x)
を使う。
ci <- mean(x) - c(d[2],d[1])
ci## 90% 10%
## 49.167 68.500
一般的にはブートストラップ分布の形状(例えば釣鐘状かどうか)、分布の中心が初期標本から得た統計量(例えば平均値)に近いかどうか等を調べるが特に統計量のバイアス(偏り)が注目される。θ^-θの分布はθ^*-θ^の分布と近似しているすればブートストラップ経験分布から信頼区間を計算できる。
よくブートストラップを使った論文等でシミュレーション回数(リサンプル数)を1999とか9999に設定しているものを見かける。不思議に思っていたが、このようにすると切りの良いパーセンタイルを計算できるということらしい。ブートストラップ法で得たブートストラップ推定値を昇順に並べ、例えばリサンプル数1999であれば0から1999までの2000の数字のうち、もし97.5パーセンタイル点を求めるならば2000×0.975=1950という切りのいい整数を得て1950番目の数値が97.5パーセンタイルに対応する推定値となる。プロの統計分析家の仕事は芸が細かいと感心した次第である。(If
a number of bootstraps is 1999,sorting the bootstrap estimates from smallest
to largest,the 1950th value is 97.5% percentile)
パッケージboot(using resampling method D)を使っても以下のように同様の結果を得る。いづれにしてもシミュレーション回数が10,000回になるとバイアスがかなり小さくなっており標本平均の精度は高そうに見える。
#パッケージbootを使って同様の
#シミュレーション10,000回
nsims=10000
set.seed(123)
zz1 <- boot(x,boot.mean, R = nsims)
mean(zz1$t) #標本平均の平均値
## [1] 58.866
sd(zz1$t) #標本平均の標準誤差
## [1] 7.5217
mean(zz1$t)-mean(x) #偏り(バイアス)
## [1] 0.032267
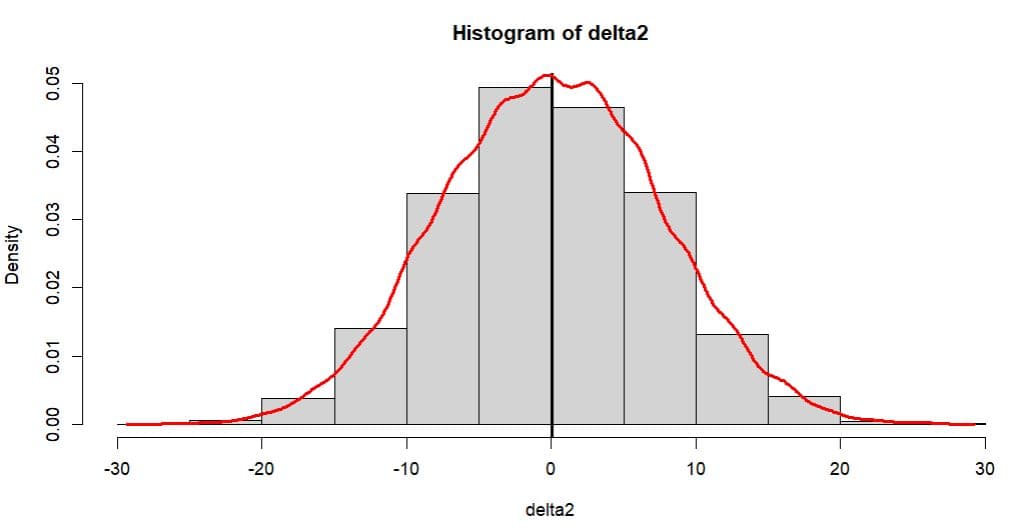
delta2 <- zz1$t - mean(x) #偏り(バイアス)
hist(delta2,prob=T)
abline(v = mean(delta2),lwd=3)
lines(density(delta2,kernel="gaussian"),
lwd=3,col="red")
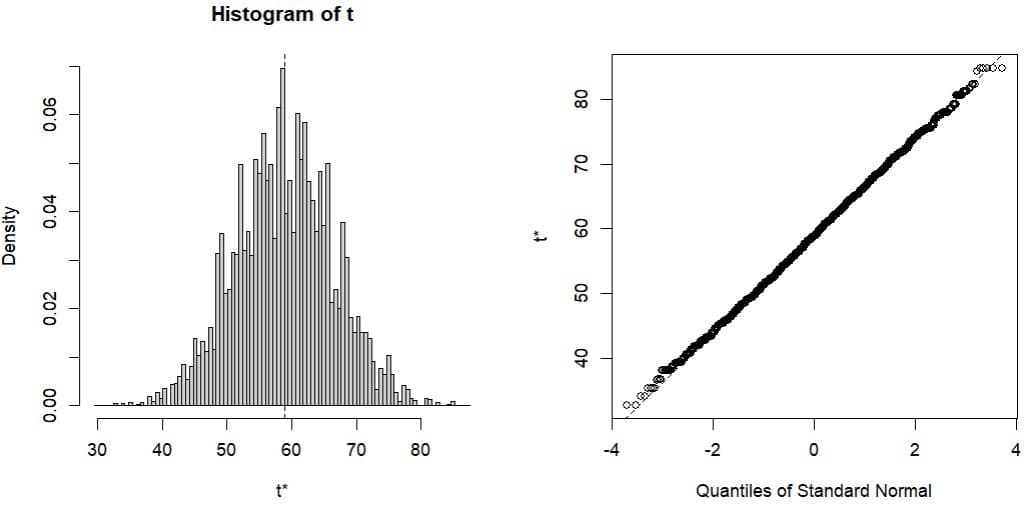
plot(zz1)
zz1
##
## ORDINARY NONPARAMETRIC BOOTSTRAP
##
##
## Call:
## boot(data = x, statistic = boot.mean, R = nsims)
##
##
## Bootstrap Statistics :
## original bias std. error
## t1* 58.833 0.032267 7.5217
boot.ci(zz1, conf = 0.80,type = "basic")
## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 10000 bootstrap replicates
##
## CALL :
## boot.ci(boot.out = zz1, conf = 0.8, type = "basic")
##
## Intervals :
## Level Basic
## 80% (49.17, 68.50 )
## Calculations and Intervals on Original Scale
上記のグラフで見るとバイアスの分布は正規分布に近似している。
中心極限定理の視覚的な理解(the merits of bootstrap simulation)
The bootstrap makes difficult concepts concrete and visual such as
the central limit theorem, standard error,etc. Not many people can understand Lyapunov's proof
of the theorem, but it is easy for many people to understand the graphical
bootstrap simulation of the theorem)
中心極限定理に関してはリアプノフはこのように証明していると聞かされてもちんぷんかんぷんだが、グラフか何かで視覚的に説明されると分かったような気がしてくる。
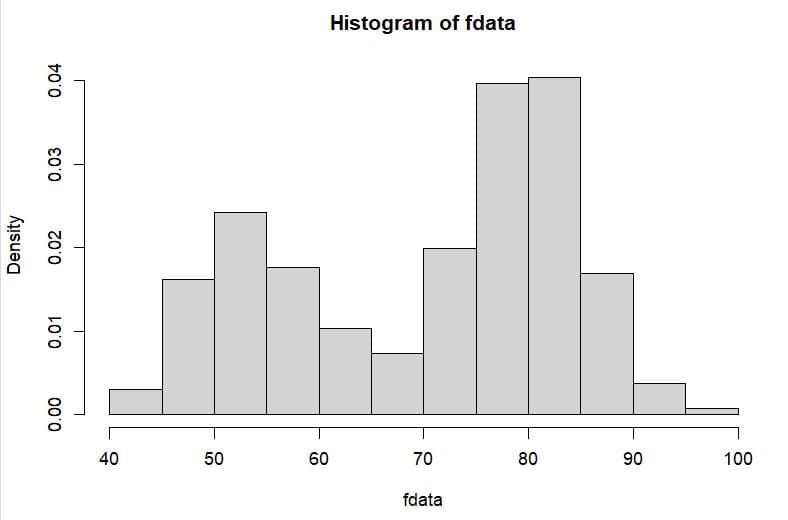
Rには統計学のテキストに出てくるサンプルデータが標準で多数準備されており、その一つにイエローストーンの間欠泉の待ち時間がある。このデータを度数分布表にすると2つの山がある分布となっており、およそ釣鐘状の形にはほど遠い。しかしその標本平均についてブートストラップ法でシミュレーションしてみると標本平均が正規分布の形状に近づいてくるのが面白い。
#####間欠泉の待ち時間
#Rに標準のデータセットとして装備されているので直ぐに呼び出せる。
data(faithful)
head(faithful)## eruptions waiting
## 1 3.600 79
## 2 1.800 54
## 3 3.333 74
## 4 2.283 62
## 5 4.533 85
## 6 2.883 55
fdata <- faithful$waiting
hist(fdata,prob=T,breaks=15)
mean(fdata)
## [1] 70.897
sd(fdata)
## [1] 13.595
sd(fdata)/length(fdata)^0.5
## [1] 0.82432
boot.mean <- function(x,i){
boot.mean <- mean(x[i])}
set.seed(123)
nsims<-10000
zdata <- boot(fdata,boot.mean, R = nsims)
mean(zdata$t)
#標本平均の平均値
## [1] 70.895
sd(zdata$t) #標本平均の標準偏差
## [1] 0.81786
mean(zdata$t)-mean(fdata)
#
偏り(バイアス)
## [1] -0.0021971
zdata
##
## ORDINARY NONPARAMETRIC BOOTSTRAP
##
##
## Call:
## boot(data = fdata, statistic = boot.mean, R = nsims)
##
##
## Bootstrap Statistics :
## original bias std. error
## t1* 70.897 -0.0021971 0.81786
hist(zdata$t,prob=T)
abline(v = mean(fdata),lwd=3)
lines(density(zdata$t,kernel="gaussian"),
col="red",lwd=2)
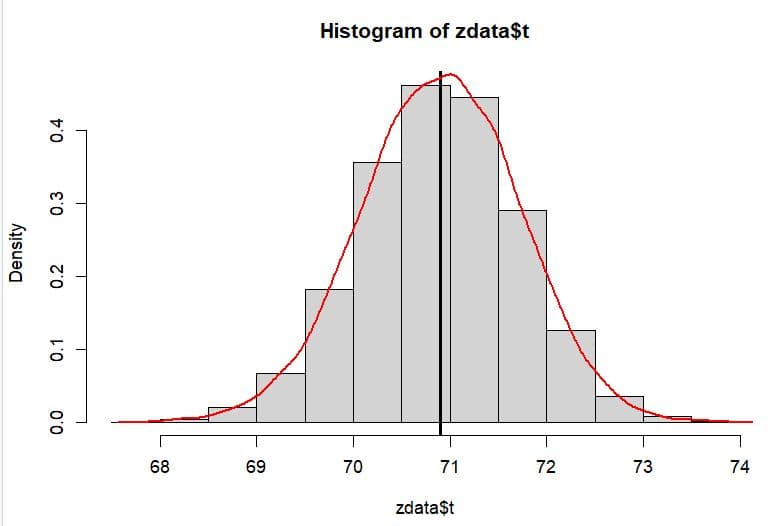
plot(zdata)
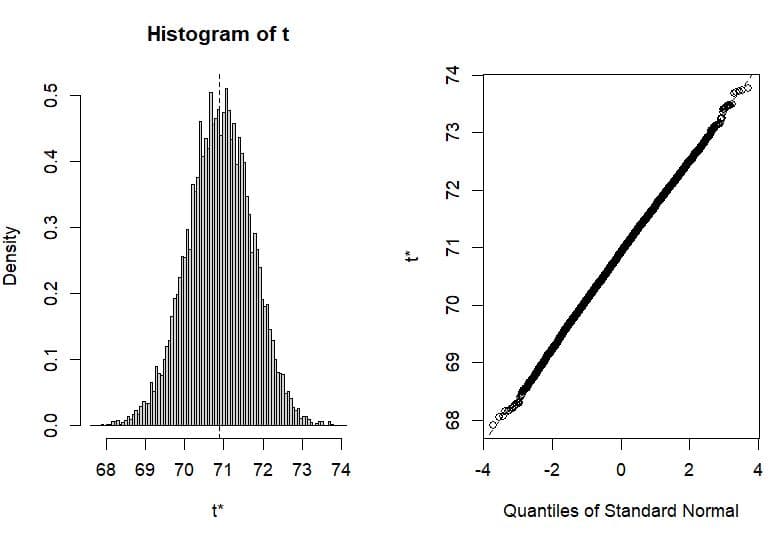
標本平均の度数分布やQQプロットで見ても綺麗に直線の上に乗っており正規分布に近似していることが分かる。初期サンプルから理論公式で求めた標準誤差は0.82432 であり、他方、ブートストラップ法のシミュレーションで得た標準誤差は0.81786 とよく近似している。ブートストラップ法で中心極限定理を具体的に体感することができる。
モンテカルロ法---πの近似計算の速度比較computing
pi using Monte Carlo in
R.
簡単な財務モデルでモンテカルロ・シミュレーション with R simple financial model using Monte Carlo
simulation with R