分位点回帰quantile regression
Rによる簡単な計算例
分位点回帰quantile regression のあらまし
分位点(分位数、quantile)とうい用語にはなじみが薄くてもメディアン(中位数)はよく知られている。メディアンは観測値を最小値から最大値に向けて大きさの順に並べた時にその観測データを2つのグループに等分する境界点の値をいう。データ数Nが奇数であれば(N+1)/2 番目の観測値、Nが偶数であればN/2番目と(N/2+1)番目の観測値の平均値 がメディアンとなる。観測値xを小さなものから順にx(1)、x(2)、x(3)...とすればx(i)はi番目の順序統計量という。任意の整数kに等分する順序統計量をk分位数というよんでいる。経験分布を求めるときには順序統計量が利用される。分位点(分位数)と同様にパーセンタイルという用語もよく使われる。例えば、観測値として100個ある場合、10パーセンタイルは小さい数値から数えて10番目に位置し、50パーセンタイルであれば小さい方から数えて50番目に位置し、これは四分位数でいえば第2四分位数に相当し、いづれもメディアンと同じになる。エクセルのようなソフトによっては0パーセンタイルは観測値の最小値、100パーセンタイルは最大値を指すこともある。
観測値に極端に大きな数値や小さな数値(外れ値という)が存在したりして分布の裾が少し厚みがあるようなデータでは通常の平均値だけでは特徴をつかみきれないことがある。金融関係のデータでは分布の裾が少し厚みがある(fat
tail)事例が多いことも知られている。そのようなときに観測値を例えば10分位点に区分して何かの特徴が把握できるかもしれない。分位点回帰は分位点ごとの関係性を明らかにし、しかも外れ値の影響を受けにくいといった利点がある。
下図のような Y- a + bX といった単純回帰を例にすれば最小2乗法は説明変数x
が与えられた時、被説明変数であるy の条件付期待値、E[y|x]を誤差項などに一定の確率分布の仮定をおいて、定数aや係数bを推定する。

最小2乗法の考え方は周知のように誤差項の2乗和が最小となるようなa,bを求める。上図でいえばu1,u2といった誤差項(残差)の2乗を合計して2乗和が最小となるようにパラメータを推定する。式で示せば下記のようになる。

上記とは異なるアプローチとしては、誤差項の2乗ではなくて誤差項の絶対値の合計が最小となるような定数aや係数bを推定する方法も考えられる。u1,u2,などの絶対値を合計して、それが最小となるようなパラメータを推定する方法である。これを最小絶対偏差推定(LAD)とうい。式で示せば

LAD推定量は最小2乗推定量に比べると統計的特性が十分に解明されていない難点はあるがブートストラップ法などで例えば誤差項の疑似サンプルを発生させて定数aや係数bを反復計算して経験分布を求めて信頼区間なども計算できるので実用的なツールとされている。この最小絶対偏差推定(LAD)に下記の式のように重みつ付けて分位点ごとのLADを計算する方法がある。これは分位点回帰とよばれている。pパーセンタイルごとの回帰係数を推定しようとすれば下式からパラメータを求める。

pパーセンタイルにおける係数a、bを a(p)、b(p)で表すと

パラメータの推定には上記のような制約条件付きの線形計画法を解くことでパラメータの推定値が得られる。直感的に表現すれば散布図(縦軸y、横軸x)のイメージでいえば次のようにして効率的に推定値を求めている。例えばp=0.1の場合は推定した回帰直線よりも下方にある観測値に0.9のウエートを付け、回帰直線よりの上方にある観測値に0.1の重みを付けて係数を推定している。その結果として推定した回帰直線の上向に観測値の90%が点在し、つまりプラスの残差uをもつ観測値が90%となり、観測値の10%は推定された直線の下方に点在し、つまりマイナスの残差uを持つ観測値が10%となるように推定計算をしている。このようにして各分位ごとに重みを変化させて計算する。もし、p=0.75であれば.回帰直線よりも下方にある観測値に0.25のウエートを付け、回帰直線よりの上方にある観測値に0.75の重みを付けて係数を推定している。結果として観測値の75%はマイナスの残差uをもち、観測値の25%はプラスの残差uをもつことになる。p=0.5 つまりメディアンを指定したときにはウエートは1-p=0.5 とp=0.5になり最小絶対偏差推定(LAD)

の式と同じになるので最小絶対偏差回帰はメディアン回帰とも呼ばれている。分位点回帰は、説明変数と被説明変数について特定のパーセンタイル、分位での関係をモデル化でき、外れ値値の影響を受けにくいといった利点がある。物の本によれば当初は労働経済学の実証研究で使われていたようだが歪みやfat-tail
のデータを扱うファイナンスの世界でも注目されて金融関係のデータ分析でも分位点回帰が使われるようになってきたようである。もう少し理論的に掘り下げたい場合には Roger
Koenker、Gilbert Bassett, Jr. Regression Quantiles Econometrica, Vol. 46,
No. 1. (Jan., 1978) を参照されたい。
分位点回帰の簡単な計算例
統計ソフトRを使った分位点回帰の一番のお薦めの入門書としては元祖のKOENKER によって書かれた QUANTILE
REGRESSION IN R: A VIGNETTE がRプロジェクトのサイトCRAN: http://cran.r-project.org で公表されており、分位点回帰を使ってエンゲルの法則に関する分析例が詳しく書かれている。
以下ではRのパッケージquantreg、パッケージEcdatの中にあるデータCapmを使って10分位についてβを推定してみた。Capmデータの内容の詳細は不明だが単に計算手順を示す例に使用するだけなので、rfood:食品企業超過収益率, rmrf:市場ポートフォリオ超過収益率
と見なして推定計算している。パケージquantregの中に関数rq()を使って分位点回帰を行える。通常の線形回帰で使う関数lm()と同様に関数I()が使える。例えば説明変数に市場ポートフォリオ超過収益率の2乗を使おうとすればI(市場ポートフォリオ超過収益率^2)を説明変数としてrq()の中で指定できる。
library(quantreg)
library(Ecdat)
data(Capm)
head(Capm)
## rfood rdur
rcon rmrf rf
## 1 -4.59 0.87 -6.84 -6.99 0.33
## 2 2.62 3.46 2.78 0.99 0.29
## 3 -1.67 -2.28 -0.48 -1.46 0.35
## 4 0.86 2.41 -2.02 -1.70 0.19
## 5 7.34 6.33 3.69 3.08 0.27
## 6 4.99 -1.26 2.05 2.09 0.24
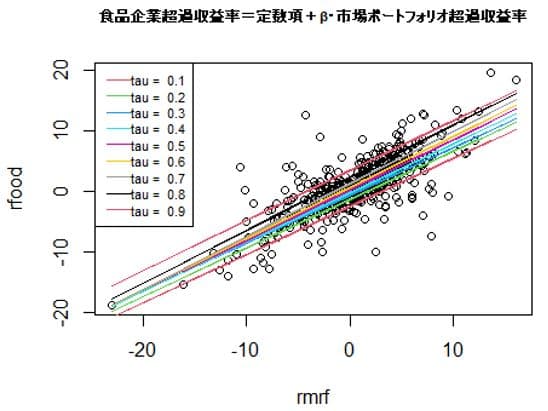
plot(rfood ~ rmrf, data = Capm,
main = "食品企業超過収益率=定数項+β・市場ポートフォリオ超過収益率",cex.main=0.7)
taus <- seq(0.1,0.9,0.1)
beta <- as.list(taus)
for(i in 1:length(taus)) {
beta[[i]] <- rq(rfood ~ rmrf, tau = taus[i], data =Capm )
lines(Capm$rmrf, fitted(beta[[i]]), col = i+1)
}
legend("topleft", paste("tau = ", taus), inset = .0,x.intersp=0,cex=0.7,
col = 2:(length(taus)+1), lty=1)
rq(rfood ~ rmrf, tau = taus[1:length(taus)],
data = Capm)
## Call:
## rq(formula = rfood ~ rmrf, tau = taus[1:length(taus)], data = Capm)
##
## Coefficients:
##
tau= 0.1 tau= 0.2 tau= 0.3 tau= 0.4 tau=
0.5 tau= 0.6
## (Intercept) -2.5025000 -1.3699608 -0.6818 -0.2890897 0.1908163
0.6240269
## rmrf 0.7934783
0.7972576 0.7850 0.8088427 0.8265306 0.8407980
##
tau= 0.7 tau= 0.8 tau= 0.9
## (Intercept) 1.2466755 2.2534 3.4341852
## rmrf 0.8677642 0.8700
0.8218054
##
## Degrees of freedom: 516 total; 514 residual
ss1<-summary(rq(rfood ~ rmrf, tau =
taus[1:length(taus)], data = Capm),se="boot")
ss1
##
## Call: rq(formula = rfood ~ rmrf, tau = taus[1:length(taus)], data = Capm)
##
## tau: [1] 0.1
##
## Coefficients:
##
Value Std. Error t value Pr(>|t|)
## (Intercept) -2.50250 0.29682 -8.43101 0.00000
## rmrf 0.79348 0.04745
16.72187 0.00000
##
## Call: rq(formula = rfood ~ rmrf, tau = taus[1:length(taus)], data = Capm)
##
## tau: [1] 0.2
##
## Coefficients:
##
Value Std. Error t value Pr(>|t|)
## (Intercept) -1.36996 0.13261 -10.33038
0.00000
## rmrf
0.79726 0.03773 21.13149 0.00000
##
## Call: rq(formula = rfood ~ rmrf, tau = taus[1:length(taus)], data = Capm)
##
## tau: [1] 0.3
##
## Coefficients:
##
Value Std. Error t value Pr(>|t|)
## (Intercept) -0.68180 0.08057 -8.46189 0.00000
## rmrf 0.78500
0.03506 22.39101 0.00000
##
## Call: rq(formula = rfood ~ rmrf, tau = taus[1:length(taus)], data = Capm)
##
## tau: [1] 0.4
##
## Coefficients:
##
Value Std. Error t value Pr(>|t|)
## (Intercept) -0.28909 0.10838 -2.66740 0.00789
## rmrf 0.80884
0.02603 31.07567 0.00000
##
## Call: rq(formula = rfood ~ rmrf, tau = taus[1:length(taus)], data = Capm)
##
## tau: [1] 0.5
##
## Coefficients:
##
Value Std. Error t value Pr(>|t|)
## (Intercept) 0.19082 0.10196 1.87140
0.06186
## rmrf 0.82653
0.02759 29.95855 0.00000
##
## Call: rq(formula = rfood ~ rmrf, tau = taus[1:length(taus)], data = Capm)
##
## tau: [1] 0.6
##
## Coefficients:
## Value
Std. Error t value Pr(>|t|)
## (Intercept) 0.62403 0.11237 5.55308
0.00000
## rmrf 0.84080
0.03741 22.47278 0.00000
##
## Call: rq(formula = rfood ~ rmrf, tau = taus[1:length(taus)], data = Capm)
##
## tau: [1] 0.7
##
## Coefficients:
##
Value Std. Error t value Pr(>|t|)
## (Intercept) 1.24668 0.14122 8.82762
0.00000
## rmrf 0.86776
0.03966 21.88003 0.00000
##
## Call: rq(formula = rfood ~ rmrf, tau = taus[1:length(taus)], data = Capm)
##
## tau: [1] 0.8
##
## Coefficients:
##
Value Std. Error t value Pr(>|t|)
## (Intercept) 2.25340 0.20740 10.86513 0.00000
## rmrf 0.87000
0.05632 15.44774 0.00000
##
## Call: rq(formula = rfood ~ rmrf, tau = taus[1:length(taus)], data = Capm)
##
## tau: [1] 0.9
##
## Coefficients:
##
Value Std. Error t value Pr(>|t|)
## (Intercept) 3.43419 0.28764 11.93920 0.00000
## rmrf 0.82181
0.06963 11.80217 0.00000
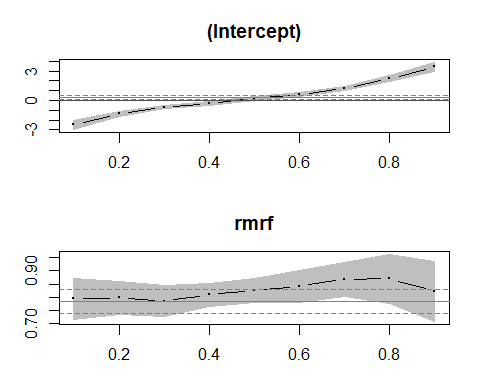
plot(ss1)
#通常の線形回帰分析
summary(lm(rfood ~ rmrf,data=Capm))
##
## Call:
## lm(formula = rfood ~ rmrf, data = Capm)
##
## Residuals:
##
Min
1Q
Median
3Q
Max
## -13.869
-1.310
-0.194
1.395
15.600
##
## Coefficients:
##
Estimate Std. Error t value Pr(>|t|)
## (Intercept)
0.33918
0.12756
2.659
0.00808 **
## rmrf
0.78342
0.02835
27.631
< 2e-16 ***
## ---
## Signif. codes:
0 '***' 0.001
'**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.885 on 514 degrees of freedom
## Multiple R-squared:
0.5976,
Adjusted R-squared:
0.5969
## F-statistic: 763.5 on 1 and 514 DF,
p-value: < 2.2e-16
通常の線形回帰で推定したβは0.78342となるが、分位点回帰では
tau= 0.1 tau= 0.2
tau= 0.3 tau= 0.4 tau=
0.5
0.7934783
0.7972576 0.7850 0.8088427
0.8265306
tau= 0.6 tau= 0.7
tau= 0.8
tau= 0.9
0.8407980 0.8677642 0.8700
0.8218054
と各分位で差異がみられる。