OTMオプションの収益率分布の自由研究 in
R
monte carlo simulation of skewed distribution of OTM option's returns in R
収益率分布の歪み
デリバティブの収益率の分布は正規分布にならず歪んでいるといわれている。
例えばOTMのオプション(コールやプットいずれでも)のロングやロング・ストラングルのポジションを持つと容易には利益を得ることは難しい。むしろ頻繁に損をすることが多く、たまにボラティリティが急増したり大きなトレンドが発生するとオプション価格が高騰して過去の損失を取り返すような経験をする
これとは別の戦略として。OTMのオプションのショートやショートストラングルのポジションを持った時には、こまめに小さな利益を得ることが多いが、たまにボラティリティが急増したり大きなトレンドが発生するとオプション価格が高騰して大きな損失をう受け過去の累積利益が消失してしまうことも経験する。
このよう二つのパターンを人為的に再現させるために歪んだt分布を使ってモンテカルロシミュレーションをしてみる。
右側に歪んだ(右方向にテールつまり尾っぽが長く伸びている分布,positive
skewnessとも呼ばれる)ケースは青色のグラフのようになる。
これとは逆に左方向にテールが長く伸びている分布(negative
skewnessとも呼ばれる)のケースでは赤色のグラフのように表される。
つまり、skewed
t分布のグラフは以下のように表される。
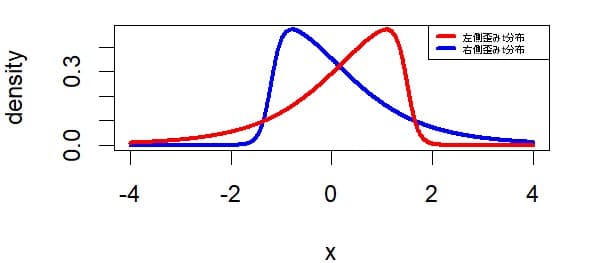
右側に歪んだt分布(青色のグラフ)のケース
右側に歪んだt分布の乱数を発生させ1万回のシミュレーションを行った結果、以下のような分布を得た。
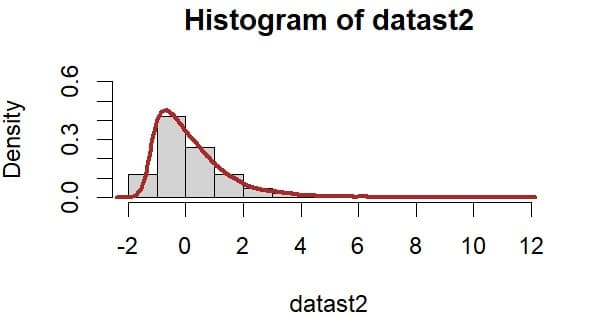
この分布の収益率の平均値は0.2、その標準偏差は1.27 で中央値は-0.11 となる。平均値はプラスであるがメディアンを見ると-0.11なので損失の機会が多いのだろうと予想できる。
左側に歪んだt分布(赤色のグラフ)のケース
同様にして左側に歪んだt分布の乱数を発生させ1万回のシミュレーションを行った結果、以下のような分布を得た。
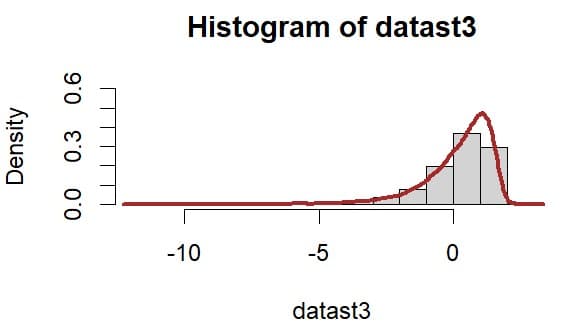
この左に歪んだ分布の収益率の平均値は0.197でその標準偏差は1.28となる。メディアンは0.52とかなり高くなり利益を得る機会が多いのだろうと予想できる。
2つの事例はかなり極端なケースかもしれないが収益率の平均値と標準偏差は同程度である。
果たして投資家はどちらを選好するだろうか。
収益率の期待値や標準偏差だけなく何か追加の指標が必要になってくるだろう。その一つの指標としてLPM(lower partial
moment)が考えられる。LPM等については
準分散、ソルティノレシオ、LPM、UPMの計算例 in Excel
参照
拙文を書くのに使ったRコードは以下のとおり。パッケージsnは歪んだt分布の生成に,パッケージe1071 は歪度、尖度の計算のために利用した。
library(sn)
library(e1071)
set.seed(123)
x= seq(-4,4, length=1000)
plot(x, dst(x, xi=-1.2,omega=1.5,alpha=8,nu=5),
ylab='density',
type ='l', col='blue',lwd=3)
lines(x, dst(x, xi=1.5,omega=1.5,
alpha=-8,nu=5), col='red',lwd=3)
legend("topright",
legend = c("左側歪みt分布","右側歪みt分布"),
lty=c(1,1),lwd=c(3,3),
col = c("red","blue"),cex=0.4)
set.seed(123)
datast2<-rst(n=10000, xi=-1.2, omega=1.5,
alpha=8,nu=5)
hist(datast2,freq=F,ylim=c(0,0.6))
lines(density(datast2),lwd=3,
col="brown",ylim=c(0,1))
range(datast2)
mean(datast2)
median(datast2)
sd(datast2)
kurtosis(datast2)
skewness(datast2) #右に歪んでいる
#### left skewed
set.seed(123)
datast3<-rst(n=10000, xi=1.6, omega=1.5,
alpha=-8,nu=5)
hist(datast3,freq=F,ylim=c(0,0.6))
lines(density(datast3),lwd=3,
col="brown",ylim=c(0,1))
range(datast3)
mean(datast3)
median(datast3)
sd(datast3)
kurtosis(datast3)
skewness(datast3) #左に歪んでいる
参考文献
Nawrocki, D. (1999) A Brief History of Downside Risk Measures. The
Journal of Investing