GARCHの初歩への道
GARCH(1,1)とGARCH-Mの初歩
This presents garch(1,1) and garch-M using
simple R code examples
GARCH(1,1)とGARCH-M の入門的なモデルの推定についてまとめてみた。
登山にたとえれば、山岳ガイドが登山口で基本的事項を説明するようなものではなく、最寄り駅に降り立った登山客に行きずりの人が登山口はあちらの方ですよと話すような内容となっている。
ARMA過程などRを使った時系列分析の基礎を無料で学ぶには
Rob J Hyndman先生のサイトが分かりやすく、個人的に気に入っている。
という専門書が https://otexts.com/fpp2/ で公開されているが、ボラティリティモデルは扱われていない。
GRACH(1,1)について
収益率retの誤差項eが以下の条件に従って時間と共に変動するモデルGARCH(1,1)を考える。数式でまとめると以下のようになる。
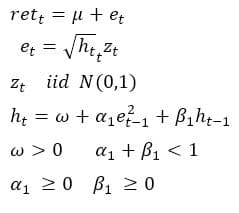
株式収益率のデータについてGARC(1,1)のモデルをあてはめてみる。
length(SP500)
## [1] 2780
ret<-ts(SP500)
garchspec1 <- ugarchspec(
##
## *---------------------------------*
rhat1 <- garchFit1@fit$fitted.values
plot.ts(rhat1,ylim = c(-1, 1))
推定結果は以下のようになり,係数の推定値はｔ値が大きく有意となっている。μ= 0.0553 ω= 0.0043
α=0.0478 β= 0.9481
ret=0.0553 + 誤差
h(t)=0.0043+ 0.0478×誤差（t-1)^2 + 0.9491×h(t-1)
と推定されている。無条件分散は ω/（1-α-β）≒ 1.048
rugarchには予測モデルも作れるので,10期先までの単純な予測を試みると以下のようになる。
fmodel
<- ugarchforecast(garchFit1,n.roll=10,n.ahead=10,data=ret)
plot(fmodel,which="all")
GARCH-M(GARCH in MEAN)モデル
収益率retの誤差項eが以下の条件に従って時間と共に変動するモデルGARCH-M(GARCH in MEAN)を考える。retの平均式の中に説明変数として条件付分散が#付け加わったモデルである。
現代ポートフォリオ理論に従ってリスクが高まればより大きな収益率が求められるという関係を示している。
ｃは追加リスクに対応するリスクプレミアムを意味している。
数式でまとめると以下のようになる。
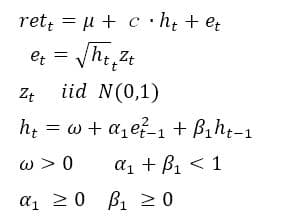
GARCH-Mモデルの平均式 retにはｈが入っているが、ｈは系列相関をもっているので、ｈの影響を受けてretも系列相関をもち、結果的に収益率は過去の収益率の影響を受ける関係を表現している。
ugarchspecの中のarchmは説明変数として条件付分散が入ることを示し、archpowは分散か標準偏差の何れかの形で説明変数にするかを表す。説明変数にｈを使うときにはarchpow=2は分散、ｈ^0.5 つまり標準偏差を使うときにはarchpow=１ と指定する。
garchSpec2 <-
ugarchspec(mean.model=list(armaOrder=c(0,0), archm=T,archpow=2),
distribution.model="norm", variance.model=list(garchOrder=c(1,1))) garchm1 <
- ugarchfit(garchSpec2, data=ret) show(garchm1)
##
## *---------------------------------*
## * GARCH Model Fit *
## *---------------------------------*
##
## Conditional Variance Dynamics
## -----------------------------------
## GARCH Model : sGARCH(1,1)
## Mean Model : ARFIMA(0,0,0)
## Distribution : norm
##
## Optimal Parameters
## ------------------------------------
## Estimate Std. Error t value Pr(>|t|)
## mu 0.023875 0.023406 1.0201 0.307700
## archm 0.052718 0.032836 1.6055 0.108378
## omega 0.004879 0.001810 2.6948 0.007043
## alpha1 0.053868 0.008483 6.3505 0.000000
## beta1 0.942488 0.009144 103.0663 0.000000
##
## Robust Standard Errors:
## Estimate Std. Error t value Pr(>|t|)
## mu 0.023875 0.024121 0.98979 0.322274
## archm 0.052718 0.035390 1.48966 0.136314
## omega 0.004879 0.002893 1.68645 0.091709
## alpha1 0.053868 0.015657 3.44063 0.000580
## beta1 0.942488 0.016832 55.99247 0.000000
##
## LogLikelihood : -3478.7
##
## Information Criteria
## ------------------------------------
##
## Akaike 2.5062
## Bayes 2.5169
## Shibata 2.5062
## Hannan-Quinn 2.5101
##
## Weighted Ljung-Box Test on Standardized Residuals
## ------------------------------------
## statistic p-value
## Lag[1] 6.738 0.009438
## Lag[2*(p+q)+(p+q)-1][2] 6.746 0.013926
## Lag[4*(p+q)+(p+q)-1][5] 12.752 0.001766
## d.o.f=0
## H0 : No serial correlation
##
## Weighted Ljung-Box Test on Standardized Squared Residuals
## ------------------------------------
## statistic p-value
## Lag[1] 0.2063 0.6497
## Lag[2*(p+q)+(p+q)-1][5] 3.1770 0.3757
## Lag[4*(p+q)+(p+q)-1][9] 3.8997 0.6059
## d.o.f=2
##
## Weighted ARCH LM Tests
## ------------------------------------
## Statistic Shape Scale P-Value
## ARCH Lag[3] 0.2614 0.500 2.000 0.6092
## ARCH Lag[5] 0.3388 1.440 1.667 0.9298
## ARCH Lag[7] 0.7099 2.315 1.543 0.9556
##
## Nyblom stability test
## ------------------------------------
## Joint Statistic: 0.9512
## Individual Statistics:
## mu 0.1997
## archm 0.1501
## omega 0.1697
## alpha1 0.3798
## beta1 0.2375
##
## Asymptotic Critical Values (10% 5% 1%)
## Joint Statistic: 1.28 1.47 1.88
## Individual Statistic: 0.35 0.47 0.75
##
## Sign Bias Test
## ------------------------------------
## t-value prob sig
## Sign Bias 0.9817 0.32632
## Negative Sign Bias 1.3957 0.16292
## Positive Sign Bias 1.8310 0.06721 *
## Joint Effect 19.3632 0.00023 ***
##
##
## Adjusted Pearson Goodness-of-Fit Test:
## ------------------------------------
## group statistic p-value(g-1)
## 1 20 72.09 4.125e-08
## 2 30 84.12 2.849e-07
## 3 40 100.09 2.849e-07
## 4 50 112.27 7.160e-07
##
##
## Elapsed time : 0.41705
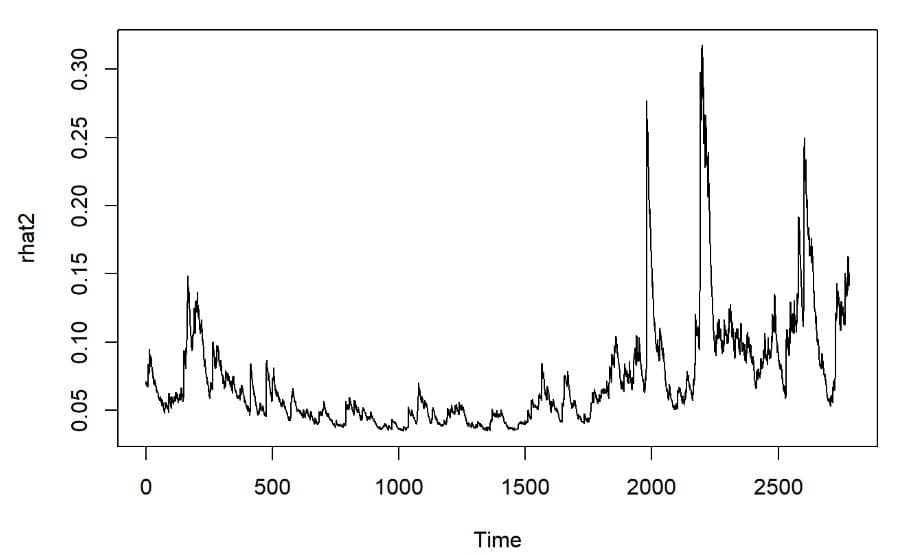
rhat2 <- garchm1@fit$fitted.values
plot.ts(rhat2)
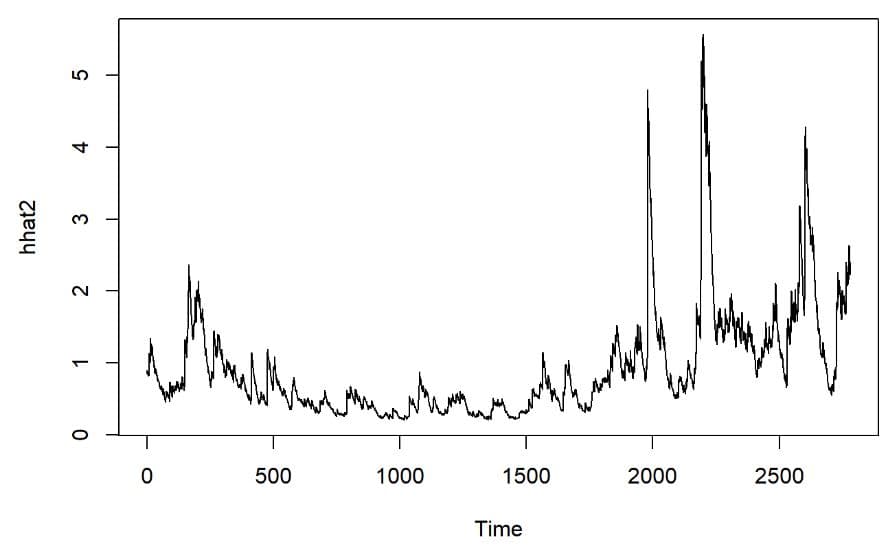
hhat2 <- ts(garchm1@fit$sigma^2)
plot.ts(hhat2)
推定結果は以下のようになり、μ= 0.0238 c=0.0527
ω= 0.0048 α=0.0538
β= 0.9424
ret=0.0238 + 0.0527×h + 誤差 h(t)=0.0048+ 0.05388×誤差（t-1)^2 + 0.9424×h(t-1)
と推定されている。
GARCH-Mモデルでは収益率も大きく変動していることが
グラフで分かる。GARCH(1,1)モデルでは平均値で一定だったが収益率がｈの影響を受けるのでGARCH-Mではボラタイルとなってる。
rugarchには予測モデルも作れるので,10期先までの単純な予測を#試みると以下のようになる。
fmodel <- ugarchforecast(garchm1,n.roll=0,n.ahead=10,data=ret)
plot(fmodel,which=c(1))
plot(fmodel,which=c(3))
rolling予測も出来るが、その場合は予測に100個のデータを使うのでout.sample=100 を指定しておく。rolling forecastについては
garchFit3 <- ugarchfit(spec=garchSpec2, data=ret,out.sample=100)
rugarchにはブートストラップ法で予測する機能もついているので１０期先までの予測を試みると以#method=c("Partial")でなくc("Full")も指定できるが、ＲのバージョンがR-4.0.2 だとエラーとなってしまう。R-3.6.2の時にはc("Full")を指定しても少々時間がかかるが計算してくれる。ちなみにrugarchのバージョンは1.4.0
を使用している。
bootp<- ugarchboot(garchm1,method=c("Partial"),n.ahead =
10,n.bootpred=100,n.bootfit=100)
bootp
##
## *-----------------------------------*
## * GARCH Bootstrap Forecast
*
## *-----------------------------------*
## Model : sGARCH
## n.ahead : 10
## Bootstrap method: partial
## Date (T[0]): 2780-01-01
##
## Series (summary):
## min
q.25 mean q.75
max forecast[analytic]
## t+1 -4.5047 -1.15111 0.001599 0.75044 5.0786
0.16023
## t+2 -2.9764 -0.65115 0.191981 1.17784 3.6243
0.15999
## t+3 -6.9669 -0.66939 0.212311 1.27388 4.9540
0.15976
## t+4 -3.1171 -0.46887 0.474701 1.33241 4.3096
0.15952
## t+5 -3.9732 -0.63170 0.119738 1.12066 3.7115
0.15928
## t+6 -3.9451 -0.48926 0.169970 1.19663 3.6684
0.15905
## t+7 -7.5622 -1.11045 -0.225839 0.68351 6.3595
0.15881
## t+8 -6.4267 -1.05151 -0.116018 0.81089 4.2977
0.15858
## t+9 -9.0114 -0.85119 0.023165 1.02170 4.9233
0.15834
## t+10 -4.0601 -0.63714 0.113709 0.96303 5.0671
0.15811
## .....................
##
## Sigma (summary):
## min q0.25
mean q0.75 max forecast[analytic]
## t+1 1.6083 1.6083 1.6083 1.6083 1.6083
1.6083
## t+2 1.5629 1.5643 1.6031 1.6127 1.9354
1.6069
## t+3 1.5192 1.5340 1.5878 1.6141 1.9043
1.6055
## t+4 1.4775 1.5184 1.5924 1.6260 2.2347
1.6041
## t+5 1.4441 1.5021 1.5868 1.6447 2.1820
1.6027
## t+6 1.4108 1.4857 1.5817 1.6618 2.1195
1.6013
## t+7 1.3939 1.4752 1.5762 1.6486 2.0811
1.5999
## t+8 1.3558 1.4553 1.5930 1.6727 2.4105
1.5985
## t+9 1.3243 1.4532 1.5894 1.6449 2.4745
1.5971
## t+10 1.2892 1.4551 1.5939 1.6481 2.6021
1.5957
## .....................plot(bootp,which=c(2))
plot(bootp,which=c(3))
