
抄録(abstract)
最尤法の考え方を視覚的、体感的に理解するために統計ソフトRを使って簡単な計算例で実験してみた。 To gain a
visual and intuitive understanding of maximum likelihood
estimation, I ran a simple example in R
最尤法をよく理解するためには統計学の専門書を熟読する以外に方法はないのかもしれないが、試しに統計ソフトRを使って簡単な計算例で計算実験しつつ体感的に最尤法の考え方を探ってみた。稚拙な感想文のようなものだが、ざっと読み流していただければと思う。(Rコードは文末に掲載)
よく教科書でベルヌーイ分布のような離散型確率分布で尤度を説明することがある。しかし、計算例などを見ても最尤法の仕組みの話につながらないことが多く直感的に理解することも難しかった。
尤度関数は、母集団の未知の母数(パラメータ)θを仮定した下で、無作為に独立に、観測された標本データ(標本要素)x1,…,xn が得られる同時確率密度を、母数θの関数とみなしたものである。
数式で示すと

尤度は離散型確率分布では尤度は確率(同時確率)と同じになるが、尤もらしさを示す指標を意味している。この同時確率密度L(θ|x1,…,xn) は標本観測値x1,…,xn に依存していると同時に母集団のパラメータθにも依存している。標本観測値xiは既に標本抽出で得た確定値なので尤度関数はパラメータθの関数とも解釈できる。そこで最尤法はθを動かして尤度Lが最大となるような統計量θ を求めようとする。言い換えると、標本観測値を既に与えられたものとしてθを変化させL(θ|x1,…,xn) が最大となるようなθを最尤推定量とする考え方である。
100個の電球が入った箱には良品と不良品が含まれているが、その割合は不明である。そこで、無作為に3個を抽出したところ、(良品、良品、不良品)となり1個が不良品だった。(話と単純にするためサンプル数を3個としている)
良品には0、不良品には1を与えて、この箱の不良品率pを推定したい。電球の状態は良品か不良品かの何れかであり、これはベルヌーイ分布に従うと考えられる。
ベルヌーイ分布の確率関数(probability mass
function)はf(x;p)=px(1-p)1-x x=0, 1
で表せる。目的とする事象は出現する(成功)か、出現しない(失敗)かの二者択一なので、事象が出現した(成功の)場合には1、出現しない(失敗の)場合には0をとる。パラメータpは不良品率としているので不良品が見つかれば成功で1、良品であれば失敗で0とする。
3個のサンプル調査で(良品、良品、不良品)の標本が実現したとすればx=(0,0,1) となる。
1番目のサンプル(標本要素)は良品なのでx=0
その確率はf(x;p)=p0(1-p)1-0 =1-p
2番目のサンプル(標本要素)も良品でx=0 その確率はf(x;p)=p0(1-p)1-0 =1-p
3番目のサンプルは不良品なのでx=1
その確率はf(x;p)=p1(1-p)1-1 =p
先ほどの定義で 尤度関数 L(θ|x1,…,xn)
は、以下の積の形で表される。

最尤法はこの同時確率(連続型確率モデルでは同時確率密度)が最大になるようなpを求めて、これを最尤推定値とする。この尤度関数はL(p)=(1-2p+p2)p=p-2p2+p3 で表されるので、この関数をpで微分して最大値となるpをL'(p)=1-4p+3p2=0 として求める。これを解くと(3p-1)(p-1)=0 よってp=1/3と1 を得る。尤度関数L(p)にこれを代入するとL(1/3)=0.148.. L(1)=0 となるのでL(1/3)=0.148という最大尤度を与えるp=1/3をパラメータpの最尤推定値とする。( 2次導関数でL''(p)=(1-4p+3p2)'=6p-4 からp=1/3の時のL''(p) <0となるのでp=1/3で最大と確認)
統計ソフトRを使って、上記のベルヌーイ分布の最尤推定値を求めた結果をグラフに表してみる。
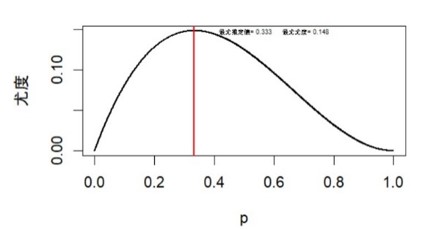
p=1/3 のところで尤度が0.148と最大になっている。最尤法は尤度関数 L(p) = p × (1 - p)2 についてpを0から1まで変化させて最大尤度0.148を与えるp=1/3をその推定値としている。観測された結果(良品、良品、不良品の同時確率)が最も起こりやすくするようなpを最尤推定値となっている。最尤法は観測データに基づき、その観測結果が最も起こりやすいパラメータを推定している。この例では観測された結果(良品、良品、不良品)が最も起こりやすくなるようなパラメータを推定している。離散型確率分布では尤度はサンプル(標本要素)の同時確率となるので下限はゼロで上限は1となる。このモデルでは尤度関数をθ 微分すると解析的にきれいな形の推定量が導出できるので、得られた最尤推定量の算式に観測値を入れて推定値が計算できる。これについては後で確かめることにする。
この最尤法の考え方は正規分布のような連続型確率モデルでも同じであるが、正規分布のような連続型確率分布では尤度はサンプル(標本要素)の確率密度の積で定義される。正規分布では確率密度の積は、下限はゼロになるが上限は1という保証はなく無限大となる。例えば正規分布で分散が限りなくゼロに近い分布の確率密度は極端に尖がり(発散し)、これらの積は極端に大きな値となりうる。
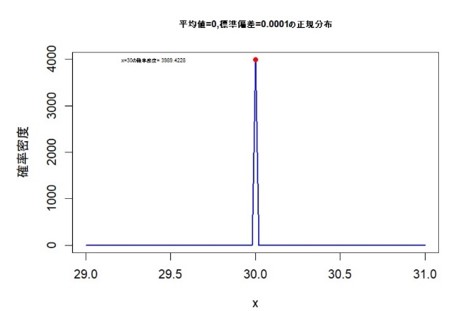
つまり上限はなく+∞の可能性がある。離散型確率分布のモデルでは同時確率になるので上限は1である点と大きく異なってくる。
正規分布の場合、尤度関数は密度の積で表現されているので、各変数xを-∞から+∞までの変域で重積分すれば1となるように思う人もいるかもしれないが、尤度関数ではそのような計算はできない。尤度関数に出てくる変数xは標本実現値であり確定値なので動かすことはできない。尤度関数で動かせる変数は母数(パラメータ)であり、例えば、ベルヌーイ分布であればp、正規分布であれば平均とか標準偏差といったパラメータが変数となる。
話を単純にするために、無作為、独立に2個のサンプルを正規母集団から抽出したとする。母集団は、平均は未知、標準偏差10で既知、の正規分布に従うと仮定する。標本要素2個からなる一組のサンプル(37,67)が得られた。
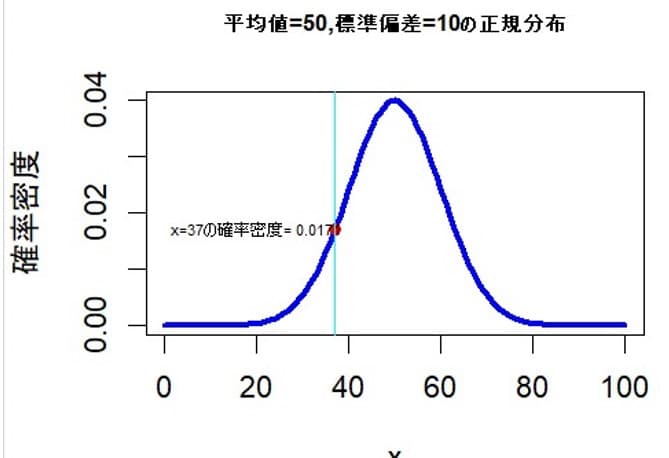
で表される。ここでθを動かして対数尤度が最大となるθを探索する。それが最尤推定値となる。ベルヌーイ分布の事例と同じ考え方である。 Rでは正規分布の確率密度はdnorm(x , mean = mu, sd = sigma)で計算できる。例えば、正規分布で x=37 平均=50 標準偏差=10の確率密度関数はdnorm(37 , mean = 50、 sd = 10)で0.01713686と計算できる。
同様にして、正規分布で x=67 平均=50 標準偏差=10の確率密度関数はdnorm(67 , mean = 50、 sd = 10)で0.009404908と計算できる。 従って

を得る。この事例では標準偏差は10と既知のため固定されているが、平均は未知のため50以外の数値をとりうる。そこで平均muを0.1から80まで0.1刻みで変化させ、800個の平均(の候補数値)について、対数尤度を800個求め、その対数尤度のうち最大値を与えるmuを平均の最尤推定値とする。Rで実験すると800の対数尤度のうち520番目の対数尤度が-8.693047と最大となり、それに対応する平均は52と計算される。この値は標本平均(37+67)/2=52 と等しくなっている。
グラフでRコードでの実験結果を示すと以下のようになる。
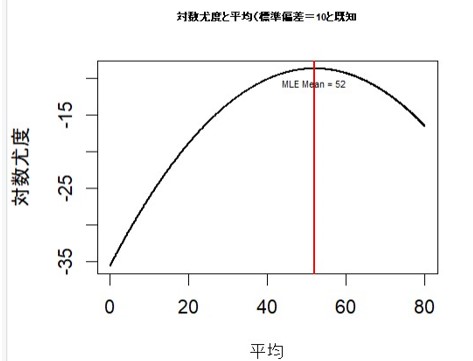
グラフでは読み取りにくいが、赤色の垂直線で対数尤度が-8.693047と最大なり、平均は52となっている。
平均も標準偏差も未知の場合の同時推定のケース
無作為に2個のサンプルを抽出したとする。母集団は、平均、標準偏差ともに未知の正規分布に従うと仮定する。 標本要素2個からなる一組のサンプル(37,67)が得られた。 この場合も同様に
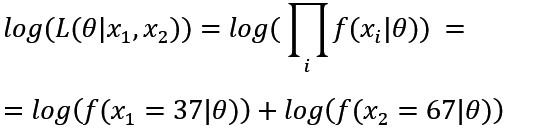
のθを変化させ最大尤度となるθを最尤推定値とする。ただし、平均と標準偏差の2つのパラメータが未知なのでθは(平均mu
,標準偏差 sd)の2要素を持つベクトルとなる。平均mu ,標準偏差
sdを同時に変化させて最大尤度となるθを最尤推定値とする。グラフにすると尤度曲面が描かれ、その最大点に対応する平均mu
,標準偏差 sdが最尤推定値となる。
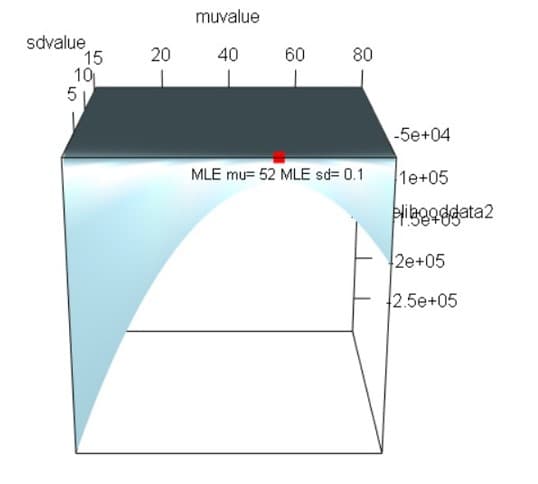
この事例では標準偏差と平均の2つのパラメータが未知である。そこで平均muを0.1から80まで0.1刻みで変化させ、同時に標準偏差sdを0.1から16まで0.1刻みで変化させる。800個の平均と160個の標準偏差について、対数尤度を128,000(=800*160)個求め、その対数尤度のうち最大値を与える平均と標準偏差のセットも求める。
Rで計算実験そしてみるとサンプル数が2個と少ないので綺麗な3次元グラフにならないが赤点の個所が最大尤度となる。
平均mu=52、標準偏差sd=15の点で対数尤度は-8.253977と最大となる。最尤法ではこれを最尤推定値とする。
最尤法の考え方を直感的に理解しやすくするために、素朴な総当たり的なグリッドサーチで推定値を計算しているが、最尤法のソフトでは効率的なアルゴリズムが開発されている。ニュートン法やBFGS法などはよく知られている。最尤法は1回で得られたサンプルから最大限の情報を引き出そうとする考え方で実務的にも広く使われている。反復実験を重視する立場では1回限りのデータに依存することを心配するが、経済事象などでは反復実験は不可能なのでブートストラップ法を併用して信頼性を補強する試みも行われている。
最尤推定量を解析的に 対数尤度関数をパラメータで微分して最尤推定量が解析的にきれいな数式(closed form)で得られれば、その推定量にサンプル値を入れてパラメータの推定値が計算できる。常に解析的に式が得られる保証はないがベルヌーイ分布に従うパラメータpや正規分布に従うパラメータ(平均と標準偏差)は解析的にきれいな数式で最尤推定量が得られる。その計算過程を以下に示す。

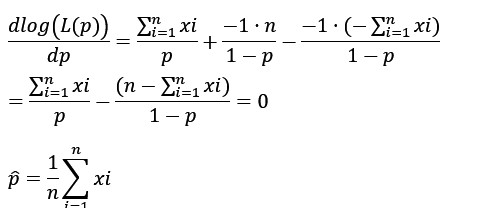

対数の法則を使って簡略化すると
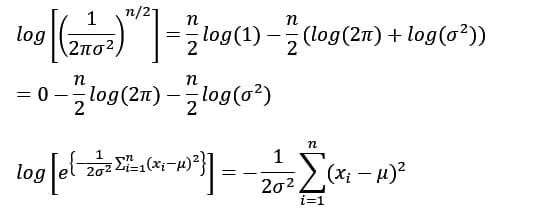
従って
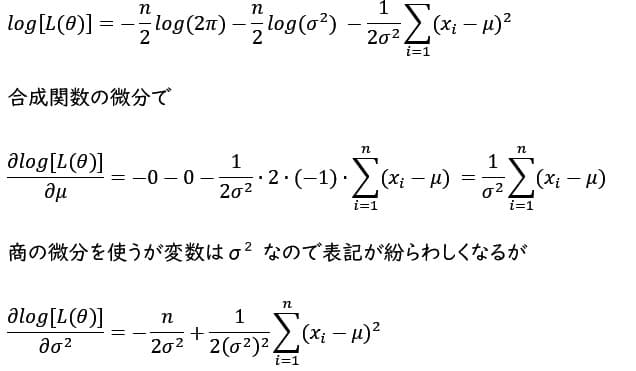


算式から明らかなように分散の最尤推定量は不偏推定量でないが、他に不変性、漸近正規性などの望ましい性質を備えていることが知られている。
平均の最尤推定量を求めたのと同じ要領で、線形の単純回帰モデルの回帰係数βを最尤法で推定するには
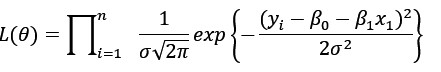
と尤度関数を定義すれば、この対数尤度関数をそれぞれの係数で偏微分して正規方程式が導出できる。(例えば参考文献3.Damodar
N Gujarati 2003 Basic econometrics 参照)
対数尤度関数を微分して解析的にきれいな数式(closed
form)で推定統計量が得られれば、その式にサンプル値を入れてパラメータの推定値が計算できる。しかし複雑なモデルになると尤度関数は解析的に最大化できないために数値計算で最適値を探索することになる。そのためBFGS,
Nelder-Mead, L-BFGS-Bなどのアルゴリズムが使われている。
ベルヌーイ分布の最尤推定
# ベルヌーイ分布の最尤推定 # 3個の製品を検査し、不良品が1個 # このときの不良品率の最尤推定値を ## x<-seq(0,1,by=0.001) bernlike<-sapply(x,function(p) (1-p)*(1-p)*p) maxpvalue<-x[which.max(bernlike)] maxpvalue maxlike<-bernlike[which.max(bernlike)] maxlike plot(x,bernlike,type="l",lwd=2, xlab="p",ylab="尤度") abline(v=maxpvalue,col="red",lwd=2) text(x=0.6,y=max(bernlike), labels=paste("最尤推定値=",round(maxpvalue,3), " 最尤尤度=",round(maxlike,3)),cex=0.4) maxpvalue
尖った正規分布
#尖った正規分布
## 極端に尖った正規分布 平均値=30,標準偏差=0.0001の確率密度は
curve(dnorm(x,mean=30,sd=0.0001),from=29,to=31,lwd=2,col="blue",
xlab="x",ylab="確率密度",
main="平均値=30,標準偏差=0.0001の正規分布",cex.main=0.8)
points(x=30,y=dnorm(x=30,mean=30,sd=0.0001),col="red",pch=19)
text(x=29.4,y=dnorm(x=30,mean=30,sd=0.0001),
labels=paste("x=30の確率密度=",round(dnorm(x=30,mean=30,sd=0.0001),4)),
cex=0.4)
正規分布で x=37 平均=50 標準偏差=10の確率密度関数のグラフ
#正規分布で x=37 平均=50 標準偏差=10の確率密度関数のグラフ
curve(dnorm(x,mean=50,sd=10),from=0,to=100,lwd=3,col="blue",
xlab="x",ylab="確率密度",
main="平均値=50,標準偏差=10の正規分布",cex.main=0.8)
points(x=37,y=dnorm(x=37,mean=50,sd=10),col="red",pch=19)
text(x=20,y=dnorm(x=37,mean=50,sd=10),
labels=paste("x=37の確率密度=",round(dnorm(x=37,mean=50,sd=10),4)),
cex=0.5)
abline(v=37,col="cyan",lwd=1)
正規分布で 平均の推定( 標準偏差は10と既知 )
# 正規分布で 平均の推定
# === サンプルデータ ===
sampledata <- c(37,67)
# 母数 平均の推定 標準偏差は10と既知
# 尤度関数を定義 ===
# 平均と標準偏差のペア(mu, sd)の尤度を計算する関数
calclikelihood <- function(mu, sd, sample) {
densities <- dnorm(x = sample, mean = mu, sd = sd, log = TRUE)
likelihood <- sum(densities)
return(likelihood)
}
# 平均値の候補を0.1から80まで0.1刻みで生成
muvalue <- seq(from =0.1, to = 80, by = 0.1)
length(muvalue)
# for loopを使って尤度データを計算 # sd=10と既知の場合
loglikelihooddata1 <- matrix(0,nrow=length(muvalue),ncol=1)
for (i in 1:length(muvalue)) {
loglikelihooddata1[i, 1] <- calclikelihood(mu = muvalue[i],
sd = 10,
sample = sampledata)
}
length(loglikelihooddata1)
# which()関数で最大値の位置を特定
maxindex <- which(loglikelihooddata1 == max(loglikelihooddata1), arr.ind = TRUE)
maxindex
max(loglikelihooddata1)
# 最大尤度のインデックス(行、列)を取得
muindex <- maxindex[1, 1]
# === 最尤推定値を特定して表示 ===
# インデックスから最尤推定値を特定
mlemu <- muvalue[muindex]
mlemu
plot(muvalue, loglikelihooddata1, type="l",lwd=2,
xlab="平均", ylab="対数尤度",
main="対数尤度と平均(標準偏差=10と既知",cex.main=0.5)
abline(v=mlemu, col="red", lty=1,lwd=2)
text(mlemu, max(loglikelihooddata1),
labels=paste("MLE Mean =", round(mlemu,2)), pos=1,cex=0.5)
平均と標準偏差の同時推定
# 母数平均と標準偏差の同時推定
# === サンプルデータ ===
sampledata <- c(37,67)
# 尤度関数は上記と同じ、ただし、sdは可変となりsd = sdvalue[j]に変更
# 平均値の候補を0.1から80まで0.1刻みで生成
muvalue <- seq(from =0.1, to = 80, by = 0.1)
length(muvalue)
# 標準偏差の候補を0.1から16まで0.1刻みで生成
sdvalue <- seq(from = 0.1, to =16, by = 0.1)
length(sdvalue)
# グリッドのすべての組み合わせに対して対数尤度を計算
calclikelihood <- function(mu, sd, sample) {
densities <- dnorm(x = sample, mean = mu, sd = sd, log = TRUE)
likelihood <- sum(densities)
return(likelihood)
}
# for loopを使って尤度データを計算
loglikelihooddata2 <- matrix(0,nrow=length(muvalue),ncol=length(sdvalue))
for (i in 1:length(muvalue)) {
for (j in 1:length(sdvalue)) {
loglikelihooddata2[i, j] <- calclikelihood(mu = muvalue[i],
sd = sdvalue[j],
sample = sampledata)
}}
length(loglikelihooddata2)
# === 最大尤度を与えるインデックスを特定 ===
# which()関数で最大値の位置を特定
maxindex <- which(loglikelihooddata2 == max(loglikelihooddata2), arr.ind = TRUE)
maxindex
max(loglikelihooddata2)
# 最大尤度のインデックス(行、列)を取得
muindex <- maxindex[1, 1]
sdindex <- maxindex[1, 2]
# === 最尤推定値を特定して表示 ===
# インデックスから最尤推定値を特定
mlemu <- muvalue[muindex]
mlesd <- sdvalue[sdindex]
# persp3d関数で3Dプロットを作成
library(rgl)
persp3d(x = muvalue, y = sdvalue, z = loglikelihooddata2,
aspect=c(1,1,1),col="lightblue")
# 最尤推定値の点を追加
points3d(x = mlemu, y = mlesd, z = max(loglikelihooddata2), col = "red", size = 10)
text3d(
x = mlemu,
y = mlesd,
z = max(loglikelihooddata2),
texts = paste("MLE mu=", mlemu,"MLE sd=", mlesd),
pos = 1,
adj = c(5, 5), cex=0.8,
color = "black"
)
mlemu
mean(sampledata)
mlesd
参考文献
1. 森田優三 1968 統計数理入門 日本評論社
2.稲垣宣生 1992 数理統計学 裳華房
3.Damodar N Gujarati 2003 Basic econometrics McGraw-Hill Companies Inc.
4.A.M.Mood,F.A.Graybill,D.C
.Bose 1963 Introduction to the theory of statistics McGraw-Hill Inc.