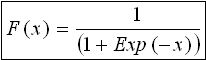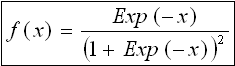-
ホーム
-
金融工学を初等数学で
-
ロジスティック方程式とロジスティック分布
ロジスティック方程式とロジスティック分布の導出 with MAXIMA
ロジスティック曲線は人口増加モデルの微分方程式から誘導され、多くの先学が各自のページで詳しく説明している。「人口増加モデル 微分方程式 ロジスティック」などと検索エンジンに打ち込めば、数学的な導出過程を説明したページが見つかる。ここでは、それらを参考にしてMAXIMAを使って
dy/dt=k*(1-y/L)*y
という微分方程式を解きロジスティック分布を導出する。
\( \DeclareMathOperator{\abs}{abs}
\newcommand{\ensuremath}[1]{\mbox{$#1$}}
\)
|
(%i2)
|
diffeq: 'diff(y,t)=k*y*(1-y/L);
sol1:ode2(diffeq,y,t); |
\[\tag{diffeq}\frac{d}{d t} y=k y\, \left( 1-\frac{y}{L}\right) \]
\[\tag{sol1}-\frac{\log{\left( y-L\right) }-\log{(y)}}{k}=t+\mathit{\% c}\]
初期値 t=0,y(t)=cとする
|
(%i3)
|
sol2:ic1(sol1, t=0, y=c); |
\[\tag{sol2}-\frac{\log{\left( y-L\right) }-\log{(y)}}{k}=\frac{k t-\log{\left( c-L\right) }+\log{(c)}}{k}\]
logを含む式を簡潔にすると
|
(%i4)
|
sol3:logcontract (sol2); |
\[\tag{sol3}\frac{\log{\left( \frac{y}{y-L}\right) }}{k}=\frac{k t+\log{\left( \frac{c}{c-L}\right) }}{k}\]
yについて整理すると
|
(%i5)
|
EQ1:solve (sol3, y); |
\[\tag{EQ1}[y=\frac{L c\, {{\% e}^{k t}}}{c\, {{\% e}^{k t}}-c+L}]\]
\[\tag{EQ2}\frac{L c\, {{\% e}^{k t}}}{c\, {{\% e}^{k t}}-c+L}\]
ロジスティック分布関数を定義すると
|
(%i7)
|
define(logist(L,k,c,t),(L*c*%e^(k*t))/(c*%e^(k*t)-c+L)); |
\[\tag{%o7} \operatorname{logist}\left( L,k,c,t\right) :=\frac{L c\, {{\% e}^{k t}}}{c\, {{\% e}^{k t}}-c+L}\]
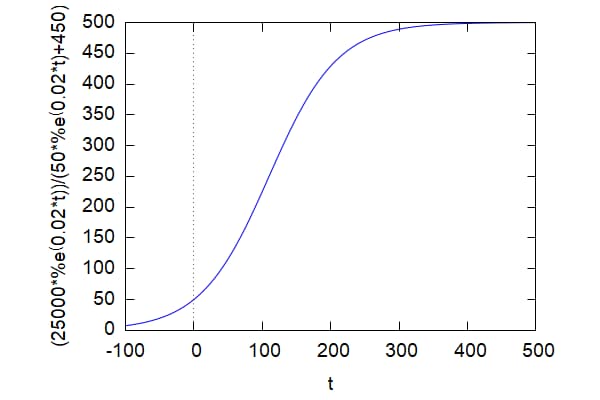
L=500,k=0.02、初期値c=50について
ロジスティック分布関数をグラフにすると
|
(%i9)
|
wxplot2d(logist(500,0.02,50,t),[t,-100,500]); |
\[\tag{%t9} \]
\[\tag{%o9} \]
ロジスティック分布関数をtで微分してロジスティック確率密度関数を定義すると
|
(%i10)
|
define(logistpdf(L,k,c,t),diff(logist(L,k,c,t),t)); |
\[\tag{%o10} \operatorname{logistpdf}\left( L,k,c,t\right) :=\frac{L c k\, {{\% e}^{k t}}}{c\, {{\% e}^{k t}}-c+L}-\frac{L\, {{c}^{2}} k\, {{\% e}^{2 k t}}}{{{\left( c\, {{\% e}^{k t}}-c+L\right) }^{2}}}\]
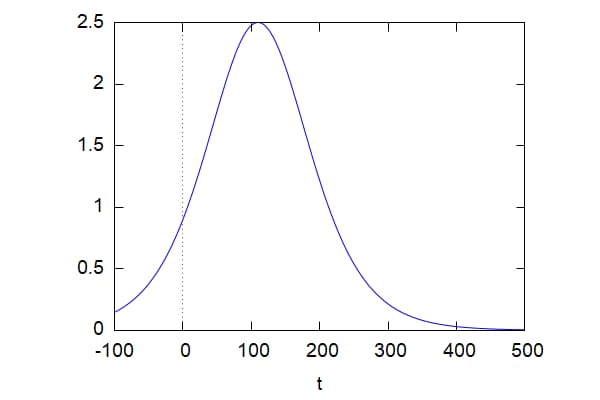
L=500,k=0.02、初期値c=50について
ロジスティック確率密度関数をグラフにすると
|
(%i11)
|
wxplot2d(logistpdf(500,0.02,50,t),[t,-100,500]); |
\[\tag{%t11} \]
\[\tag{%o11} \]
正規確率密度函数よりもすそが少し厚めで、カーブは少しなだらかになっている。
Created with wxMaxima.
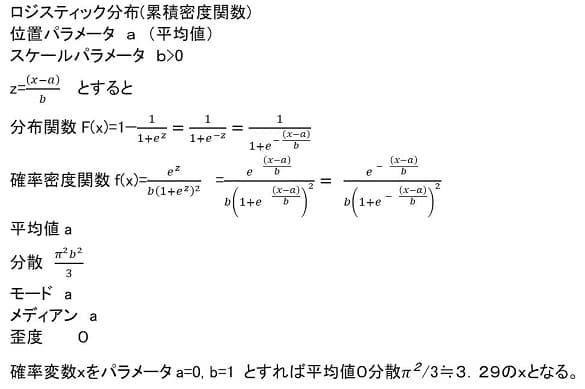
ロジスティック分布
累積密度関数
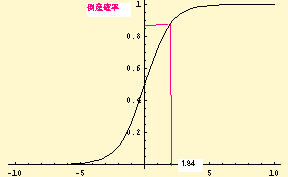
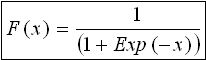
確率密度関数
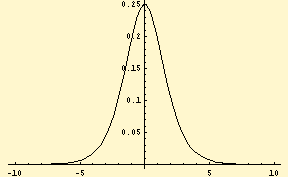
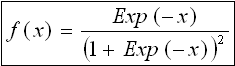
正規分布よりもすそが少し厚めで、累積密度関数のカーブは少しなだらかになっている。
期待値 E(x)=0、分散V(x)=(π^2)/3 となる。グリーン(William H
.Greene)の計量経済学テキストで少し詳しく書かれている。
ロジスティック分布の概略をまとめると以下のようになる。
金融工学を初等数学で 目次