株価指数先物と裁定取引（簡単な計算例）
simple numerical examples of arbitrage relations
特別なコスト無しに株価指数に連動する現物株ポートフォリオが何時でも構築できると仮定する。この場合には現物株ポートフォリオの価格と株価指数先物の価格のとの間で一定の関係が成立する。何等かの理由で先物価格が割高で、現物価格が割安な場合には、割高なほうを売却し、割安のほうを購入する両建のポジションを設定し、後日に正常な関係にもどったときに反対売買をしてポジションを解消することでリスクなしに裁定利益を得ることが理論的に可能となる。
このような裁定機会を判断する場合には先物価格の理論価格を把握することがポイントとなる。
株価指数先物価格の理論価格
以下では株価指数先物価格を先物価格、現物株ポートフォリオの価格を現物価格と呼ぶことにする。
一般的に、
先物価格＝現物価格＋金利
の関係が成立する。現在10,000円の現物株を１年後に受け渡しで10,000円で買いたいと申し出ても売り手は納得しないだろう。今現在、10,000円を得て、それを１年間定期預金に預ければ１年分の利息収入が得られる。もし１年後の受け渡しで株を売るならば、この利息分の補償を求めるので
先物価格＝現物価格＋金利
の関係に落ちつくだろう。しかし、株式を所有していれば株式所有者は一定の配当収入が得られるだろうから、その分だけ金利から差し引くのが理論的である。
これを算式で示すとと
先物理論価格＝現物価格＋純持越費用
純持越費用＝短期金利－予想配当
と整理される。
この算式から、株価指数先物取引では先物の最終売買日には現物価格と先物価格はSQ（最終清算指数）に等しくなるので裁定利益を捕らえることが可能となる。
この関係を以下で少し詳しく数式で調べてみる。
現物株市場と先物市場間の裁定取引
先物価格の理論価格は以下のように表せる。
先物理論価格＝現物価格＋純持越費用
から
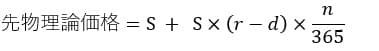
先物市場で需給関係など何等かの理由で先物の実勢価格が理論価格を上まわって
F > 先物理論価格
の状態にあれば 先物売り＋現物買 のポジションを設定することで裁定利益を得られる。
裁定利益は上式から明らかなように最終売買日の先物価格と現物価格が消去されSQ値の影響を受けていない。
投資期間利回りを計算すると
実際には取引に手数料も要し、ポートフォリオ構成等で誤差なども予想されるだろから、これらに伴う予想コストを裁定利益が上まわれば裁定取引の機会となるだろう。
もし、先物の実勢価格が理論価格を下まわって
F ＜ 先物理論価格 の場合には
先物買＋現物売り のポジションを設定して裁定取引が出来る。前記の買裁定の場合の利益Rにマイナスを乗じることで
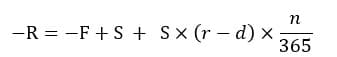
売り裁定の場合の裁定利益となる。ここでｄは品借料と読みかえる。
以下では指数先物を使った 先物売り＋現物買
の簡単な計算例を調べてみる。
先物売り＋現物買 の買裁定の簡単な計算例
現時点０での現物価格＝40,000円
短期金利 年利 ６％
配当利回り 年利 ４％
ＳＱ日まで３ヶ月（３／１２年）残されている。
と仮定すると３月限先物理論価格は40,200円となる。
（= 40,000+40,000x(0.06-0.04)x3/12)
もし、現時点（０時点）での3月限先物価格の実勢市場価格が40,300円であれば、
F(40300) > 先物理論価格(40200)
の関係となっており
割高な先物を売り、現物買のポジションを設定することで裁定利益を得られる。仮にSQ値は41,000円とする。
SQ日に反対売買でポジションを解消すると
先物決済では700円（40,300-41,000)の損失となるが
現物株売買で1,000円（41,000-40,000)の利益を得て、さらに600円の金利支払いと400円の配当収入を得る。つまり純持越費用は200円となる。これらの損益を通算すると100円(=-700+1000-600+400)の裁定利益が確定する。
一覧表にまとめると以下のようになる。
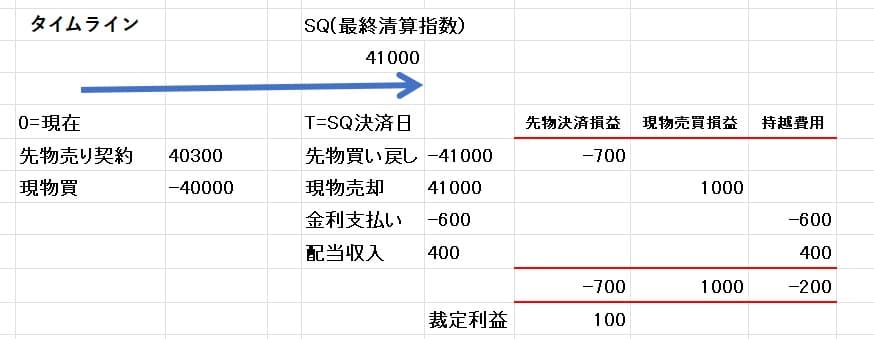
もし、SQ値が41,000円でなく38,000円であれば、やはり下図のように裁定利益は100円となる。
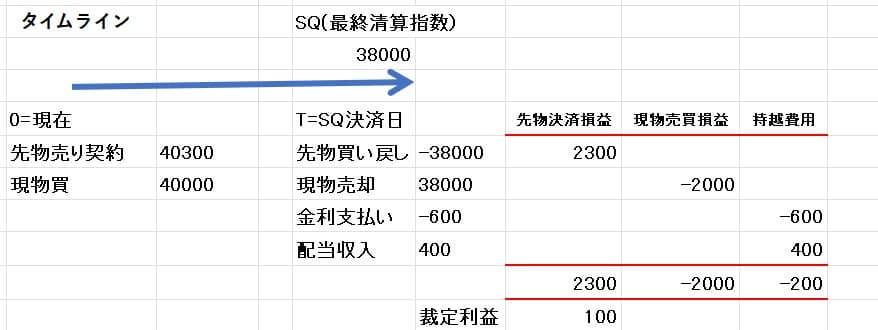
裁定取引の場合は現物価格がT時点（ＳＱ日）でのSQ値が現時点（０時点）の価格より上がっていようが下がっていようが、時価相場とは無関係に裁定利益は確定している点に注目すべきだろう。
また、ＳＱ日よりも前に需給関係などの理由で先物価格時価と現物価格時価が接近するような時には直ちに反対売買をすることで、より短い所有期間で裁定利益を確定できるかも知れない。買裁定の場合は裁定取引解消にともない現物株の売却が発生するので現物株市場での下げ圧力要因となり得る。しかしプロ投資家は先物を使ったペアトレードだけでなく合成先物とのペアトレードを実施したり、SQ日前に相対でＥＦＰ取引を行ってポジションを解消したり、あるいは先物ポジションを期先の先物にロールオーバーすることも考えられるので、実際のポジション解消の影響度を統計的に推計することはなかなか難しいようである。
ペアトレードに計量経済学の共和分回帰を使うことも考えられるが実用的かどうかは分からない。